データサイエンス 統計学 データ分析 機械学習 AI マーケティング 2024.12.24
連載！データ分析①：相関係数

連載にあたって

本連載は、一般企業に勤務し、その実務の中で、データ分析に携わる方々、とりわけ、あまり自身ではデータ分析をやったことがない、比較的初学者に向けられたものです。そのため、出来る限り数式は使用せず、感覚的にも理解しやすい形で展開していきます。

本連載で紹介するデータ分析手法は、学術的な場面でももちろんそうですが、一般企業のデータアナリストやデータサイエンティストが、実務の際に非常によく用いるデータ分析手法ばかりです。これらを身に着けておけば、データ分析にまつわる仕事をする際に、大変役立つでしょう。

記事の最後には、毎回、架空のデータを自動で作成するためのプログラムとデータ分析用プログラムを付録として掲載します。先述の通り、本連載は比較的初学者に向けて書かれています。簡単な説明はしていますが、ひとまずプログラムの文法は置いておいて、掲載したプログラムをコピー&ペーストして実行し、分析の実際を「こんな感じなのか」と味わってもらうのが目的です。

序

「自分が担当している商品の売上には、どのような要素がどのくらい影響しているのか？」 それがわかれば、マーケティング施策を変えることで、もっと売上を伸ばせるかもしれません。例えば、食品メーカーにおいては、「広告投下量を増やせば、ウチのメーカーで作っているアイスクリームがより売れるのではないか」というような仮説が生まれます。そのような仮説を、実際のデータを分析することで、その結果と照らし合わせて実証する訓練をするのが今回の連載、引いては本連載全体のねらいです。
それでは、少しの間、お付き合いいただければ幸いです。

2つの要素の間にある関係性を見る相関係数

マーケティング場面において、「売上高は〇〇千円でした」だけでは、有用な情報が得られたとは言えないでしょう。しかし、「売上高」と「広告投下量」のような2つの要素の関係を見る指標があれば、２つの要素ごとの関係性を把握することが可能であり、有用な情報を得られると言えるでしょう。

よって、ここからは、一続きになった値をもつ2つの要素について、視覚的に関係性を把握したり、全体的な特徴をシンプルにとらえる方法を紹介します(※用語については、文末の「用語集」をご参照下さい)。

散布図

2つの要素の関係を視覚的に表わす方法の1つに、「散布図」があります。散布図は縦軸、横軸にそれぞれ関係性を見たい数値を置いて、各データをプロットします。こうすることで、それぞれの要素の関係を表現できます。具体的に、いくつかパターンを示しながら説明します。

散布図から見る相関関係と相関係数

相関関係とは、2つの要素が一緒に変化する関係のことです。一方の値が増えるともう一方も増えたり減ったりする場合、それらは相関関係にあると言えます。

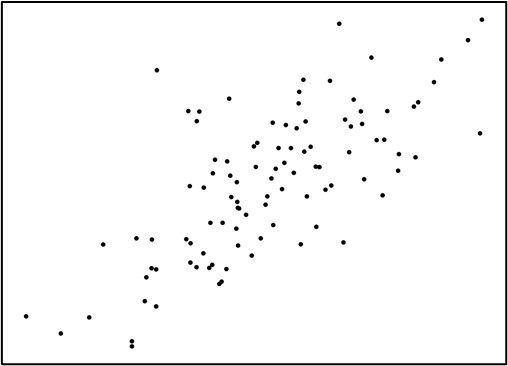
そして、その相関関係の大きさを表すのが相関係数です。相関係数とは、2つの要素の比例関係の強さを、-1.0~1.0の間の数値で表す値です。図1・2・3は、横軸の数値が高くなるほど、縦軸も高くなる傾向にあります。

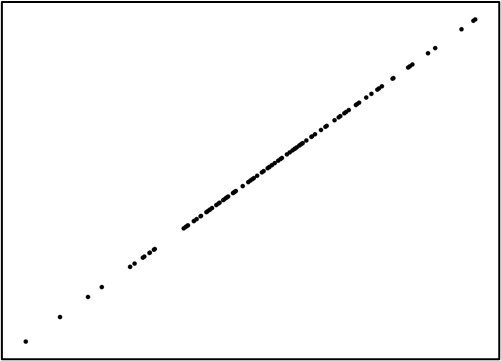
こうした関係を、正の相関関係と呼びます。図4・5・6は横軸の変数が高い値を取るほど、縦軸の数値が低くなっています。

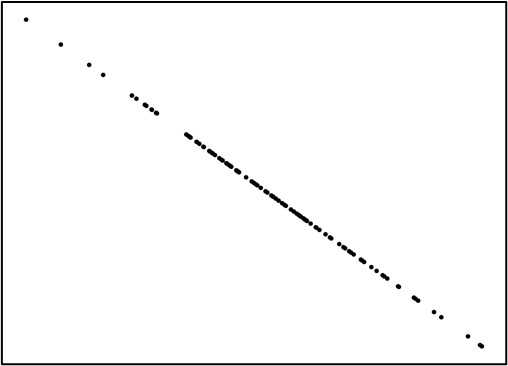
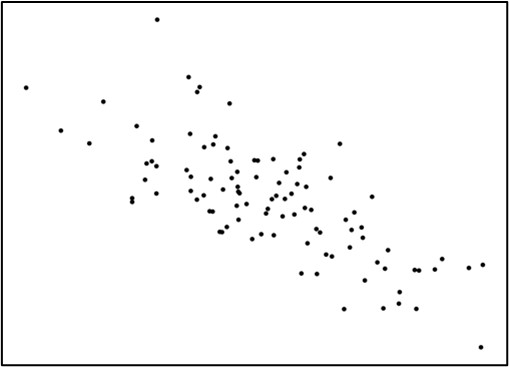
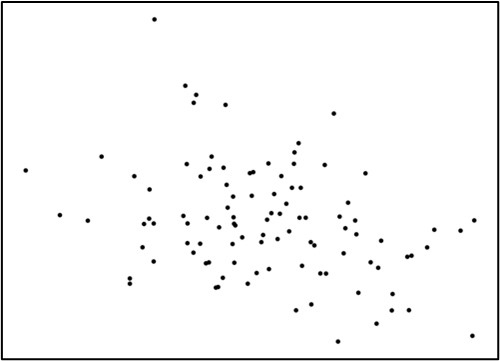
こちらは「負の相関関係」と呼びます。

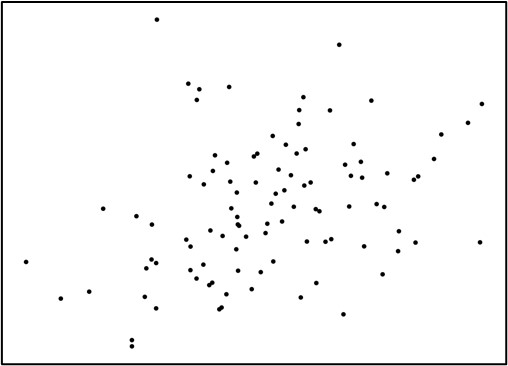
こうした相関関係とは対照的に、図7は横軸と縦軸の明確な関係が確認できません。

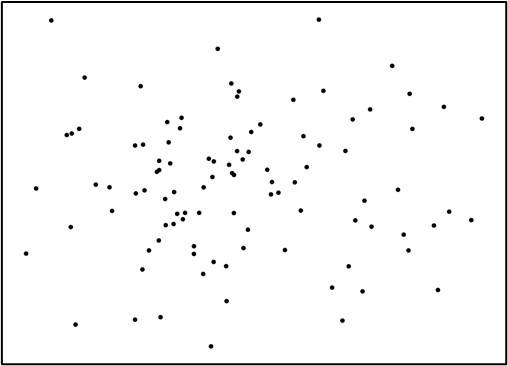
こうした状態は無相関といわれます。
また、図8は横軸が高い数値になるほど、一定の値までは縦軸の数値も高くなり、それ以降は縦軸の数値が低くなります。

こうした関係を曲線相関と呼びます。

片方の数値が「商品の魅力（良い⇔悪いを両極とする）」で、もう一方の数値が「商品の刺激の強さ（弱い⇔強い）」のときを考えてみましょう。

こうした場合、商品の刺激が弱すぎると魅力に感じず、商品の刺激が強すぎても魅力に感じないというケースがあります。結果として、強すぎず弱すぎずという「ちょうどいい」中間の刺激の強さを魅力的に感じる人が多くなり、曲線相関が発生します。

例えば、辛い系ラーメンの商品の魅力と刺激の強さ(辛さ)を考えると、人がちょうど美味しく食べられる辛さの商品が最も魅力的で、食べられないほどに辛すぎても、逆に辛さが物足りなさすぎても魅力は低減してしまう、ということを思い浮かべると分かりやすいかもしれません。(曲線相関のデータについては、取り扱いが難しいので、詳しくは本稿では省略します。)

よって、散布図でこうした関係を視覚的につかむことは、データ分析のステップとしては必須といえるでしょう。

相関係数の大きさ

先述の通り、2つの要素が一緒に変化する関係において、一方の数値が増えるともう一方の数値も増えたり減ったりする場合、それらは相関関係にあると言え、その相関関係の大きさを表すのが相関係数です。

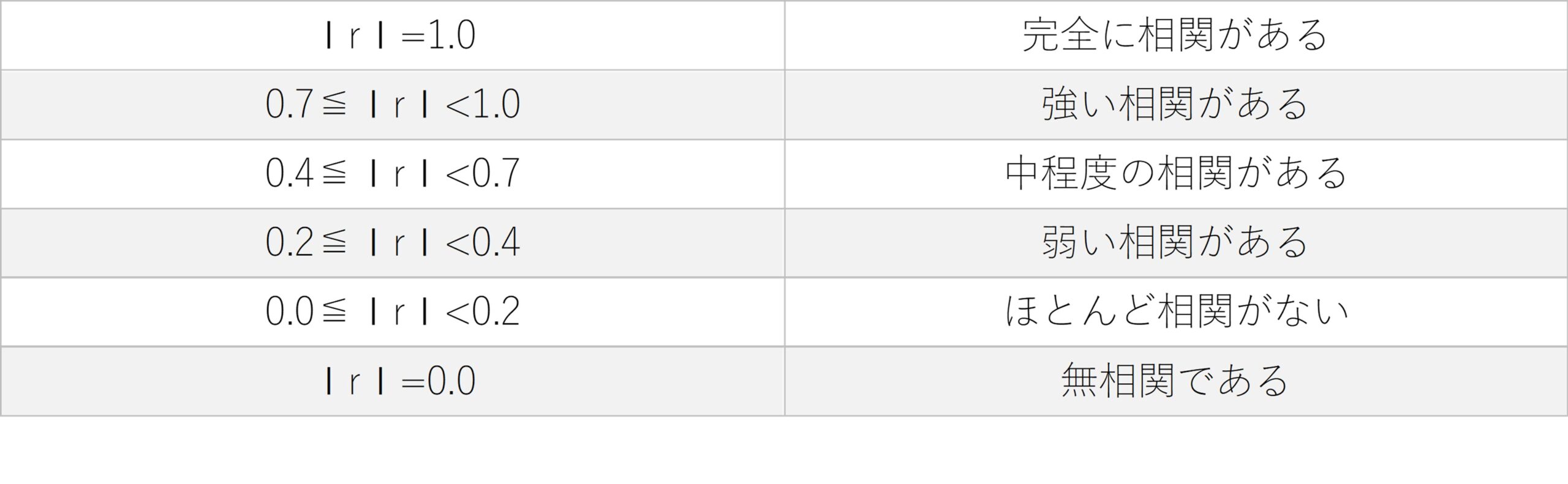
相関係数は、-1.0~1.0の間で2つの要素の相関関係の強さを表した数値です。相関関係はその大きさによって、以下のように相関係数として表すことができます(相関係数はrで表します)。

表1：相関係数の大きさ

実際に散布図で確認しておきましょう。1.0の完全な相関といえば，一直線上にデータが並ぶことを意味します。

強い相関がある，という場合は、データが直線から少し散らばっており、少々膨らんだ散布図になります。

弱い相関がある、になると、その逸脱が激しくなり、直線関係は見えなくなってきます。

無相関になると、方向性がなくなる形や円形などの形になります。

円形に散らばるデータは無相関になることも多いですが、曲線相関の場合もありますので、注意が必要です。

注意点として相関係数という指標は、2つの要素の関係がどの程度直線関係(比例関係)になっているかを示すために作られたものです。逆にいえば、曲線相関の場合など“一直線”といえないような関係があるデータに対して、相関関係を指標とするのは適していません(図9)。

相関係数による分析の仕方

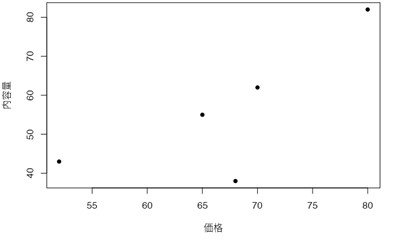
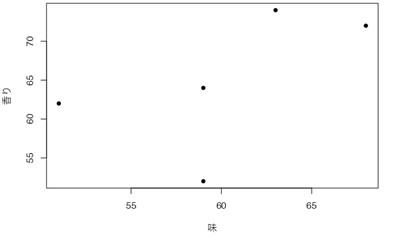
表2は、あるビールメーカーのマーケティング部が、モニターであるAさん・Bさん・Cさん・Dさん・Eさんに、新商品のビールの「価格」・「味」・「香り」・「内容量」について100点満点で評価してもらった際のスコアの一覧です。

表2：ビールの評価データ

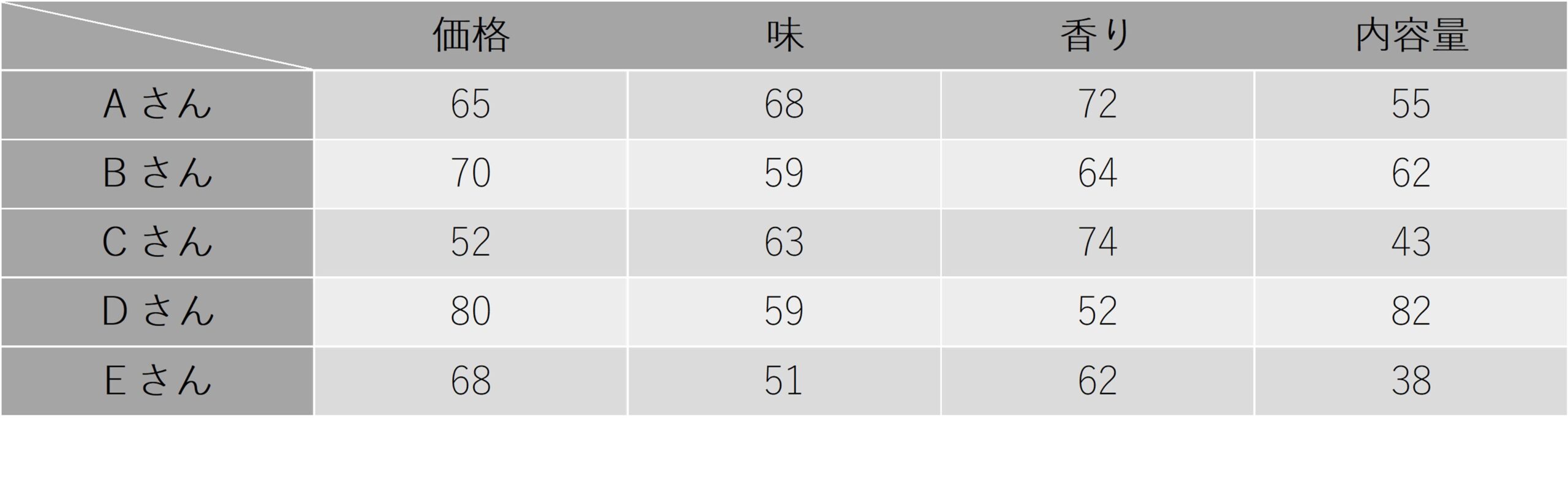
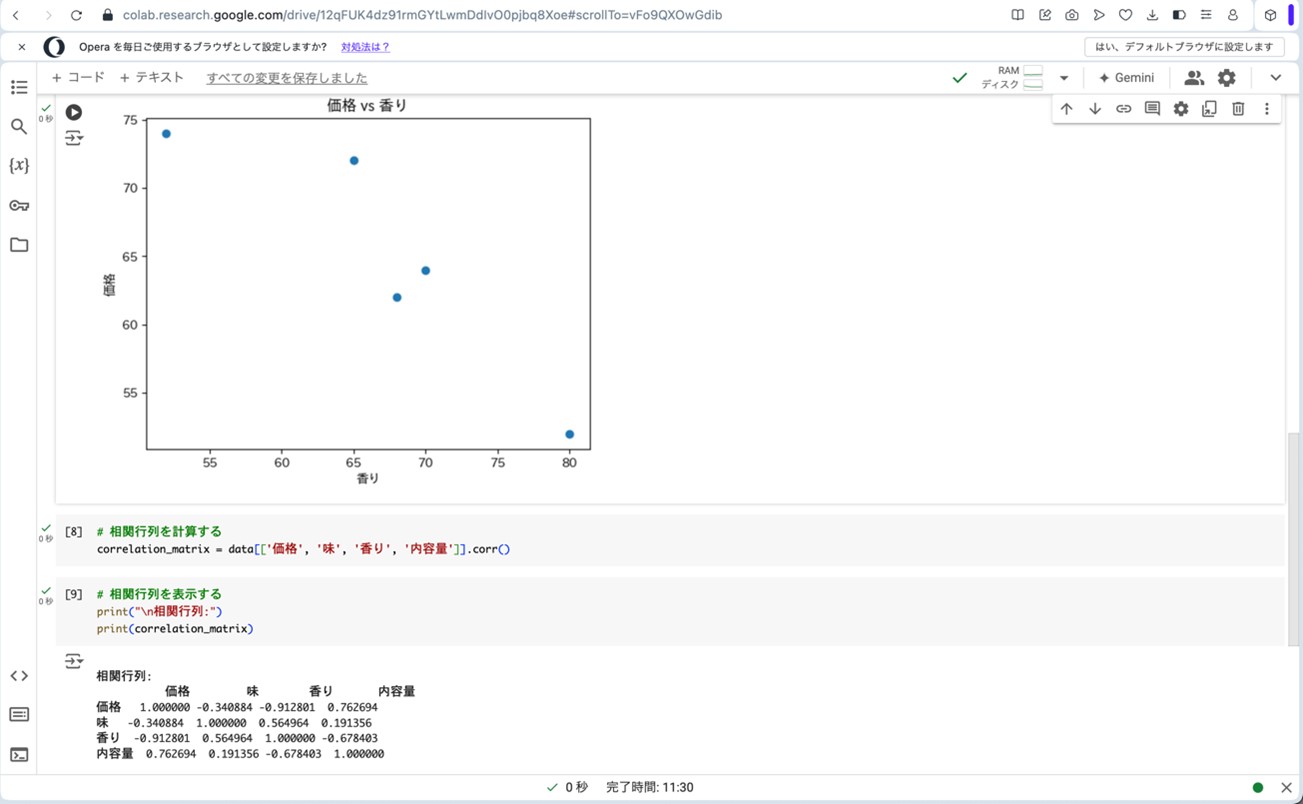
表3は、新商品のビールに対するAさん・Bさん・Cさん・Dさん・Eさんの「価格」・「味」・「香り」・「内容量」のスコア一覧(表2)から算出した相関係数を行と列に並べたものです。

表3：表2のビールの評価データから算出した相関行列

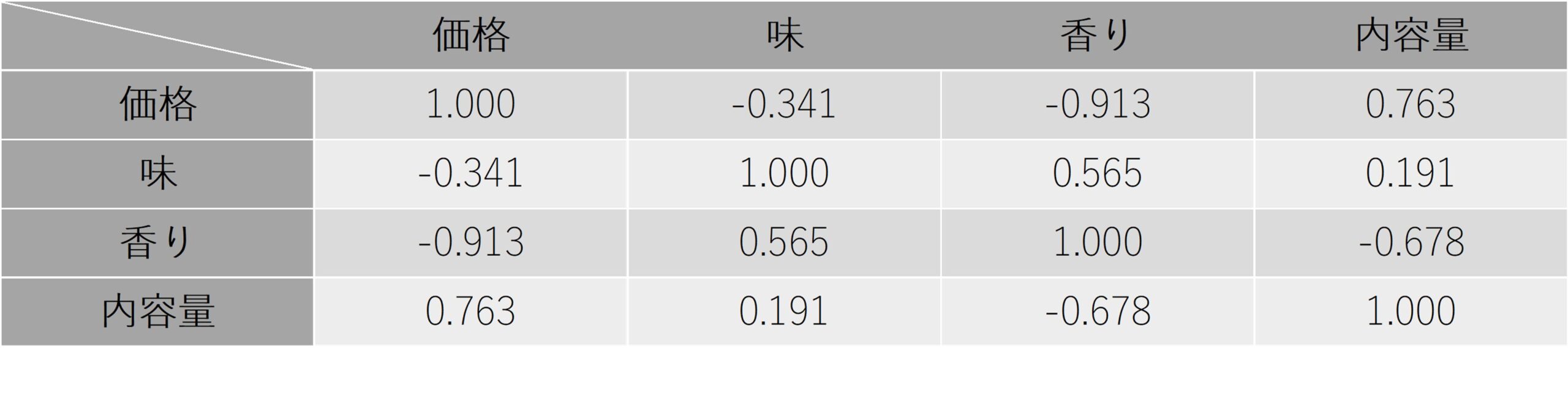
具体的には、「価格」と「味」の相関係数、「味」と「香り」の相関係数、「香り」と「内容量」の相関係数など、それぞれの相関係数を表にまとめたものです。この様な相関係数をまとめた表のことを、相関行列と呼びます。

表３の相関行列から、以下の様なことが見て取れます。

1. 価格の評価が高いと、味の評価は低くなる傾向が少しだけある(r=-0.341)。

1. 価格の評価が高いと、香りの評価は低くなる傾向が非常に強い(r=-0.913)。

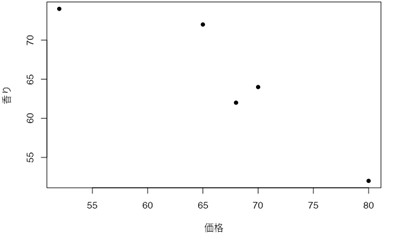
1. 価格の評価が高いと、内容量の評価も高くなる傾向が非常に強い(r=0.763)。

1. 味の評価が高いと、香りの評価も高くなる傾向がまあまあ強い(r=0.565)。

1. 味の評価と内容量の評価は、ほとんど無関係である(r=0.191)。

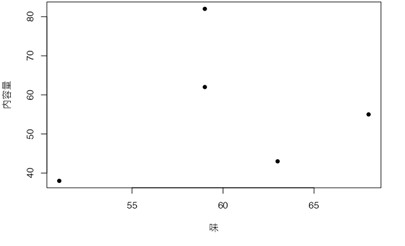
1. 香りの評価が高いと、内容量の評価は低くなる傾向がまあまあ強い(r=-0.678)。

以上のように、相関行列を用いて各要素間の関係性や特徴をつかむことを、相関分析と呼びます。相関分析は比較的簡単にデータを可視化できることから、複雑なデータ分析の下準備として行われることが一般的です。

分析環境の構築

さて、本連載の最後には、Pythonというプログラム言語を使ってデータ分析をする方法が記載されています。それには事前準備(環境構築)が必要です。

プログラムを動かすために使用するのが、Google社の提供する、Google Colaboratory とGoogleドライブです。具体的には、Google Colaboratory 上でプログラムを動かして、Googleドライブに格納したデータを呼び出して分析する、という仕組みになっています。

以下に、その事前準備の方法を解説していきます。

Googleドライブ

まずは、Googleドライブからです。Googleのアカウントを持っている人はサインイン、Googleのアカウントを持っていない人はアカウントを作成(サインアップ)し、上記のリンクからGoogleドライブに飛んで下さい。すると、図16のようなホーム画面が出てきます。

図16：Googleドライブのホーム画面

左上の『マイドライブ』をクリックすると、図17のような画面が現れます。自分で入れたファイルはまだありませんが、ここに、これからの連載ごとに使用するデータを格納していきます。

図17：マイドライブの中身

画面中央下の空白(図17の赤丸部分)を右クリックして下さい。すると図18のような表示が現れます。ここから、Google Colaboratoryの設定をしていきます。

図18：Google Colaboratoryを追加

ここで、『その他』→『アプリを追加』をクリックします。

図19：Google Colaboratoryをインストール

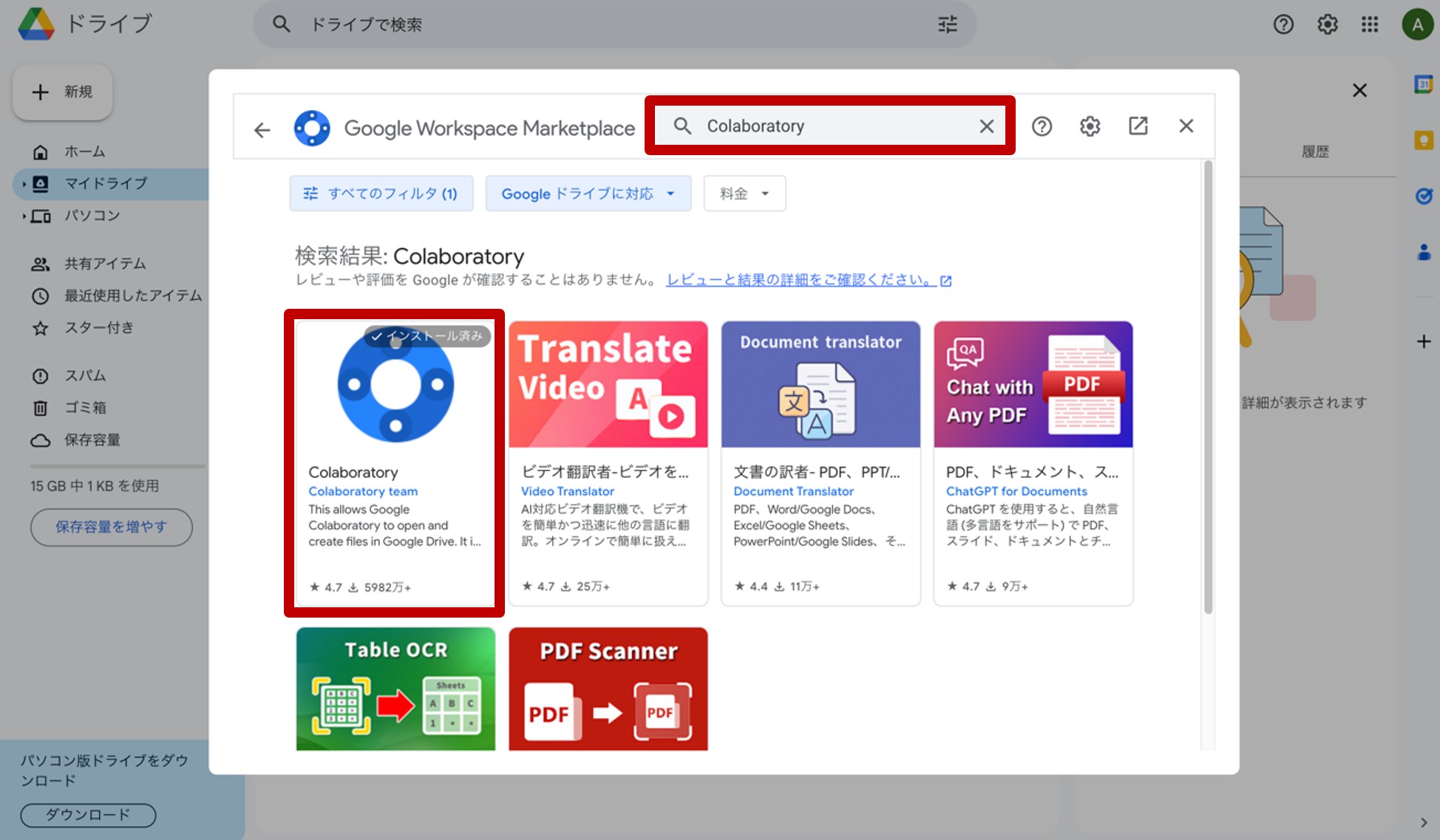
現れた画面の検索窓に『Colaboratory』と入力して検索し、インストールして下さい(図19)。以上で、Googleドライブ上での下準備は終了です。

Google Colaboratory

次に、Google Colaboratoryです。上記のリンクから飛ぶと、図20の様なホーム画面が現れます。

図20：Google Colaboratoryのホーム画面

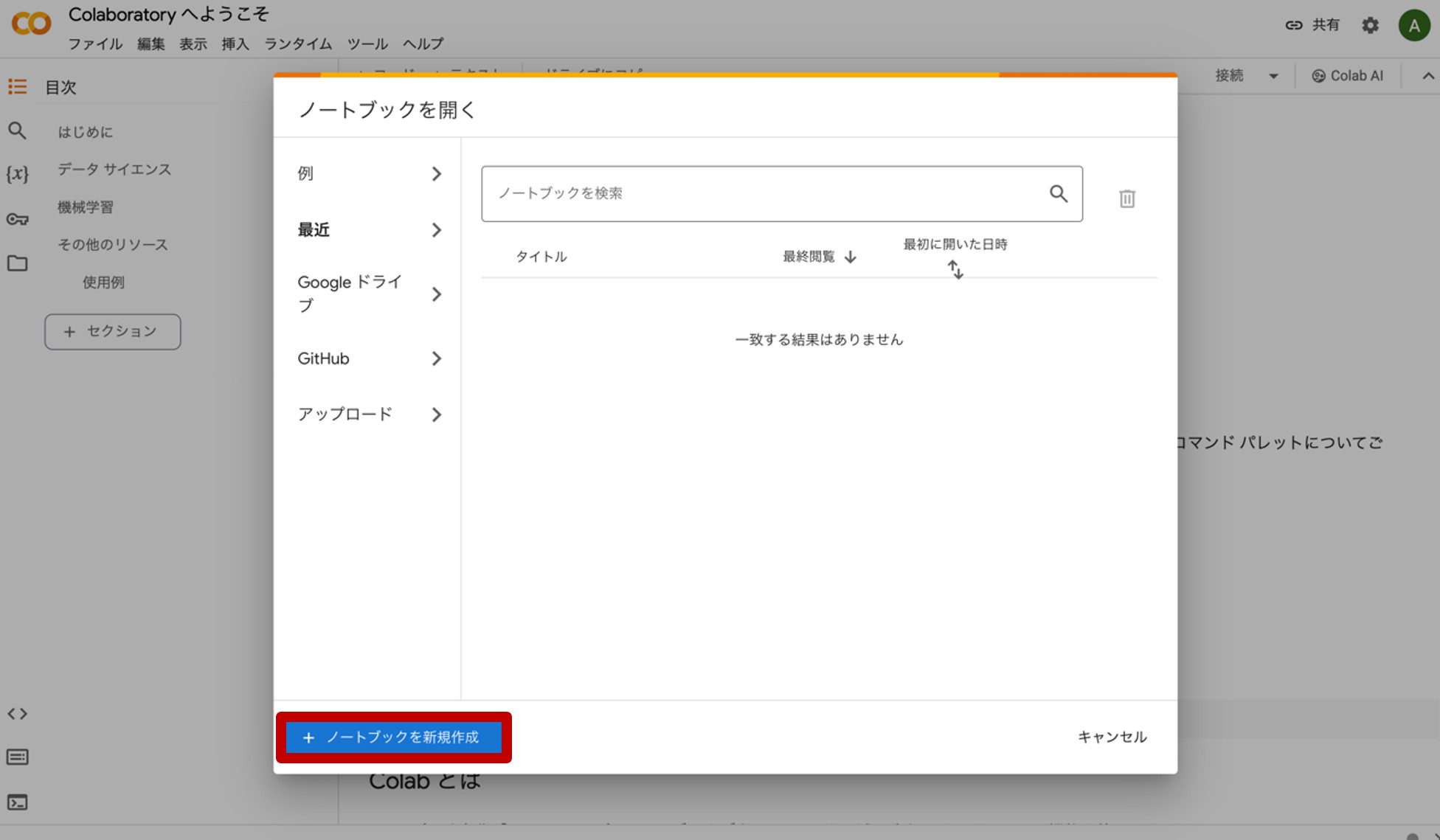
画面下側にある『ノートブックを新規作成』をクリックすると、図21のような画面が現れます。

図21：Google Colaboratoryのプログラムとテキスト入力画面

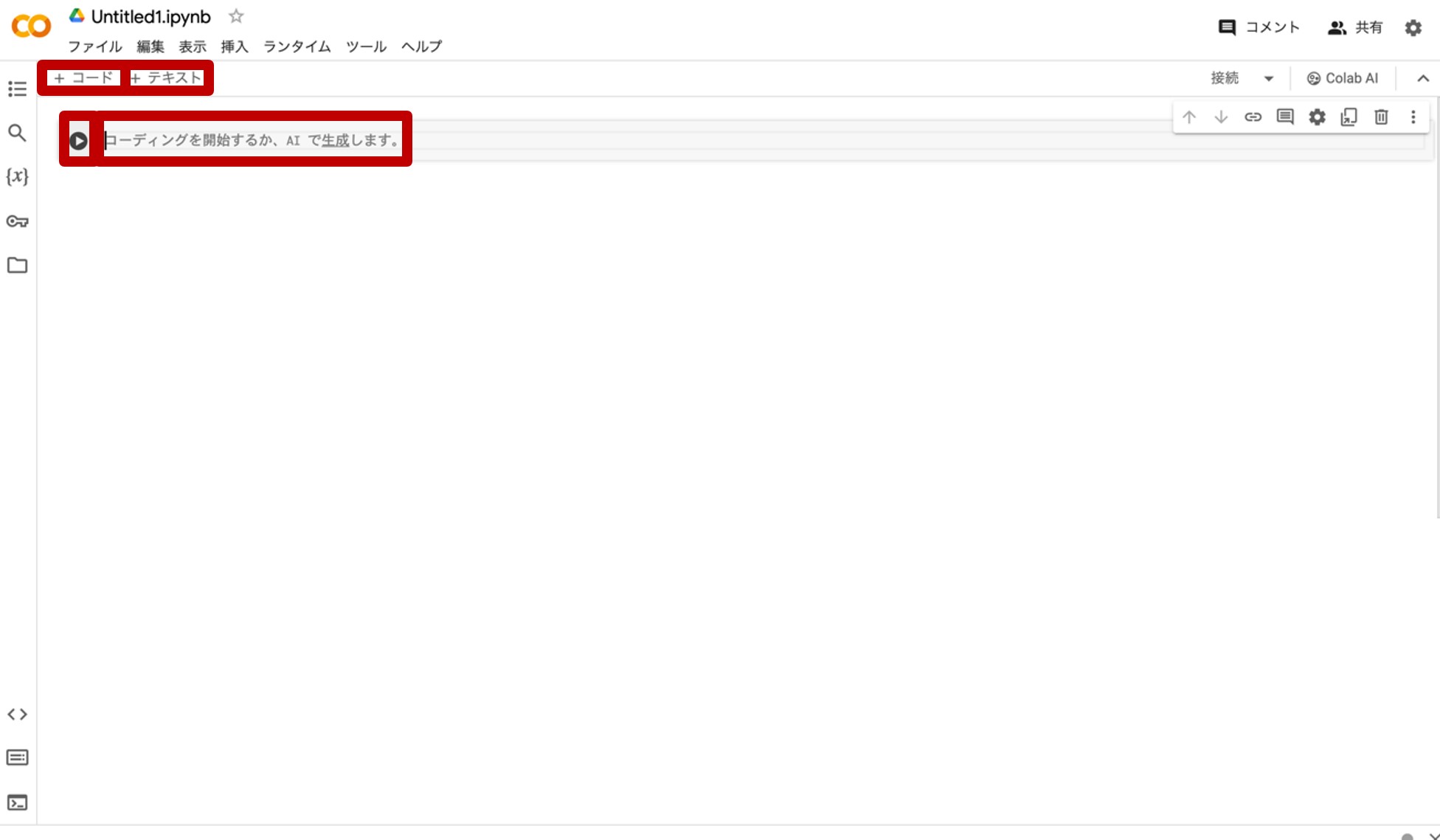
『コーディングを開始するか、AIで生成します。』(AI生成については本連載では省略します。)とあるのが、プログラムを書き込む場所であるコードセルです。左の▷ボタンを押すと当該プログラムが走り出します。分割してプログラムを書きたいときは、その上の『+コード』をクリックするとコードセルを追加することができます。
次に、『+テキスト』をクリックすると出現するのが、コードセルにあるプログラムの解説やメモを書くことができる「テキストセル」です。
以上で下準備は終了です。ここで構築した分析環境を、各連載のデモ分析の際に役立てて下さい。

実際のデータとPythonのプログラム

以下に、Pythonを用いて先ほどのビールの評価データを生成する方法と、表3の相関行列を算出するPythonのプログラムを用意しています(※Pythonとライブラリのバージョンアップによってはプログラムが動かなくなる場合があります。本記事での使用ver.はPython3.12.3、pandas2.0.3)。

実際にみなさんのお手元のPCで計算して、実際の分析がどのような感覚か、まずは直感的に味わってみましょう(プログラムの文法等はひとまず置いておきましょう。)。
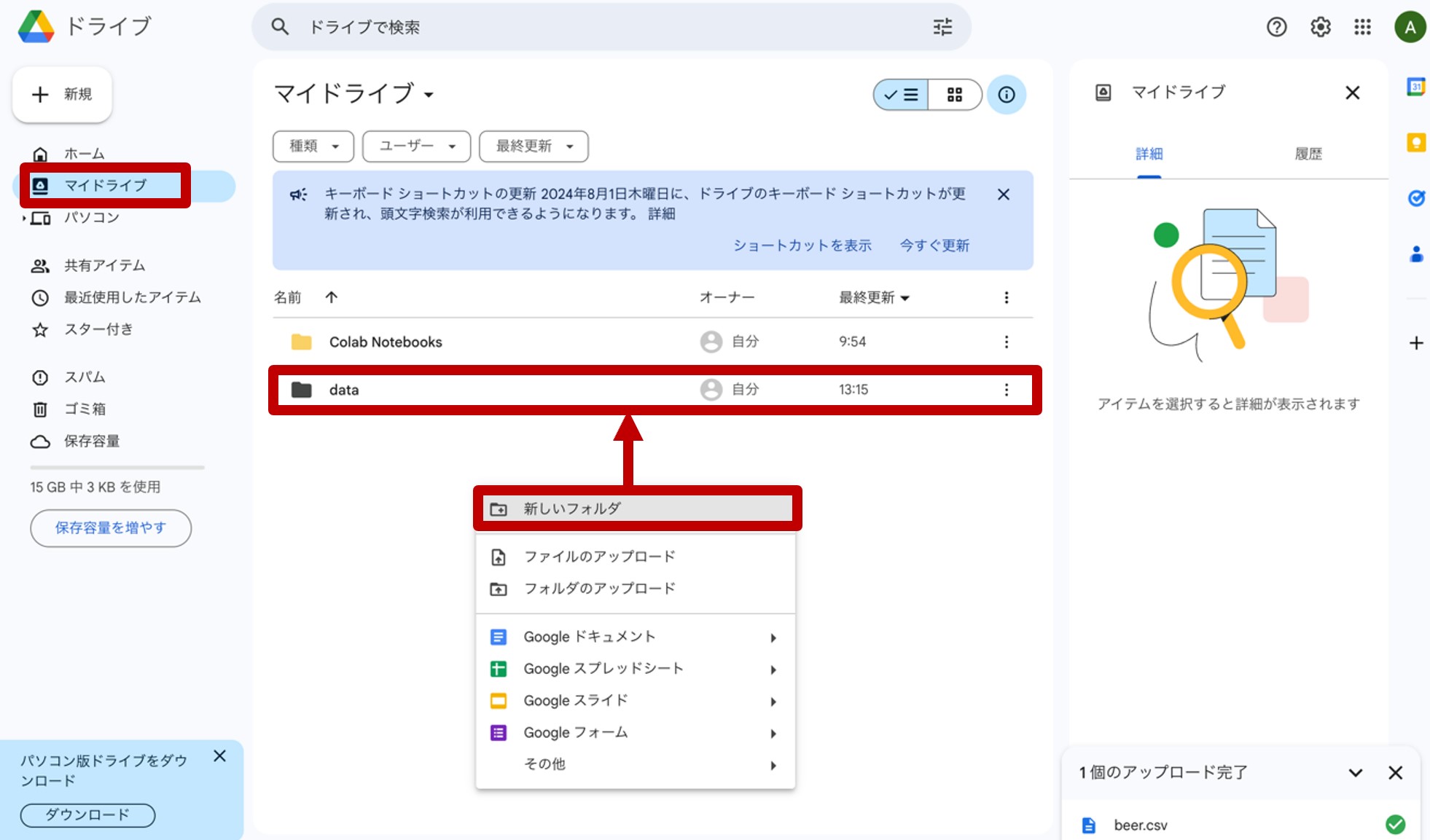
先ほどのリンクからGoogleドライブに飛び、『マイドライブ』を開きます。『マイドライブ』の空白部分を右クリックして『新しいフォルダ』を開き、「data」という名称のフォルダを作成します。(図22)

図22：マイドライブに「data」フォルダを作成

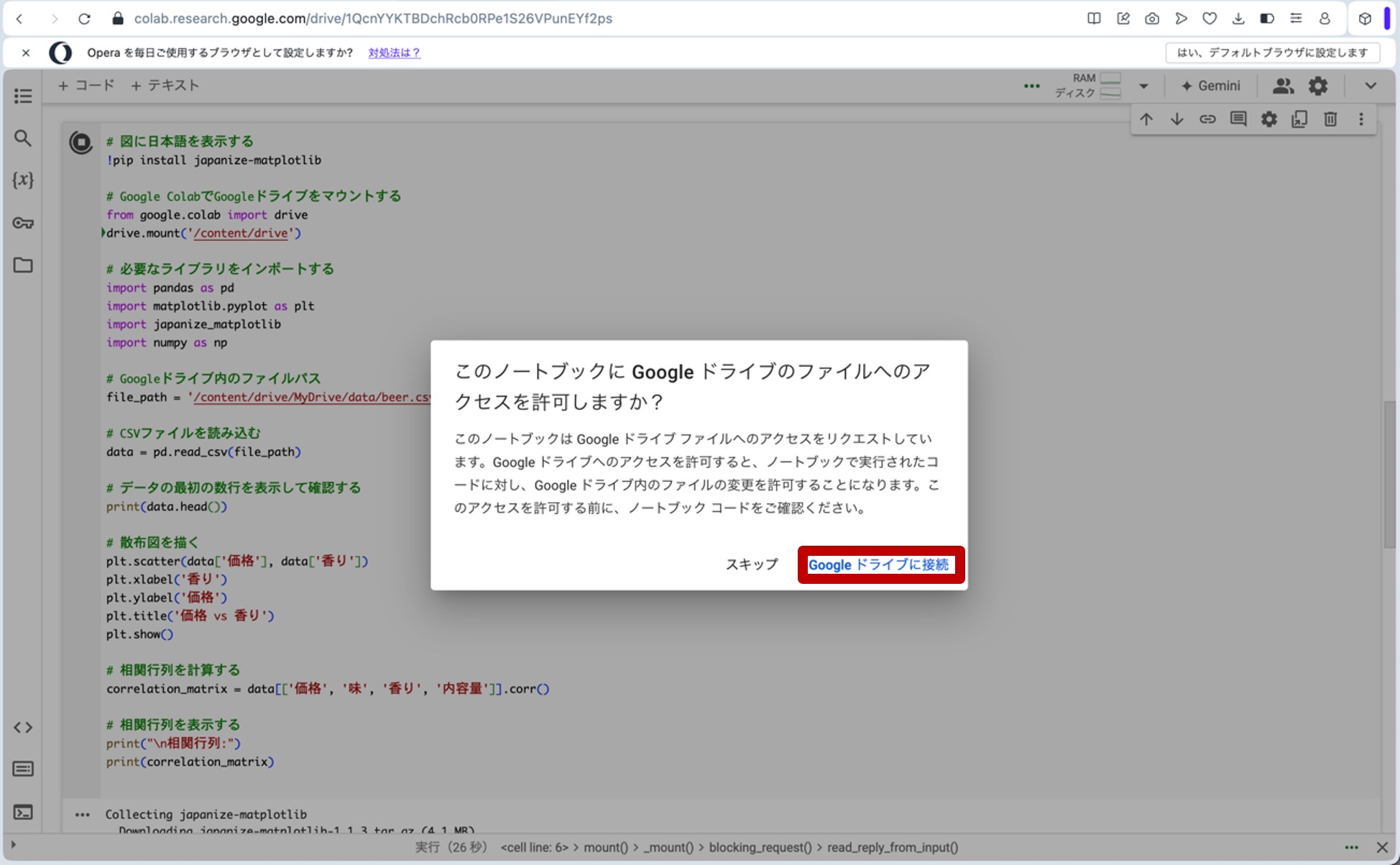
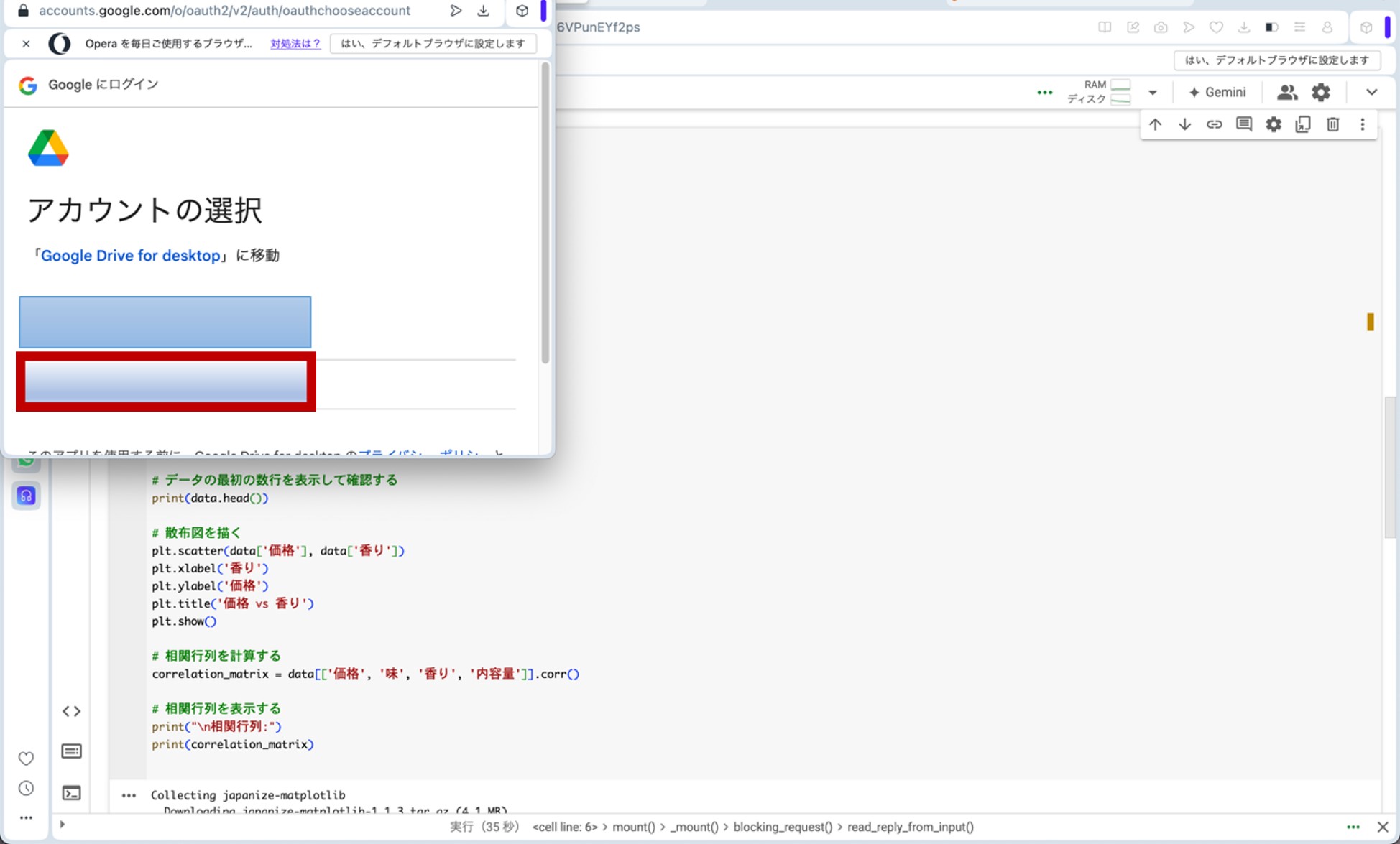
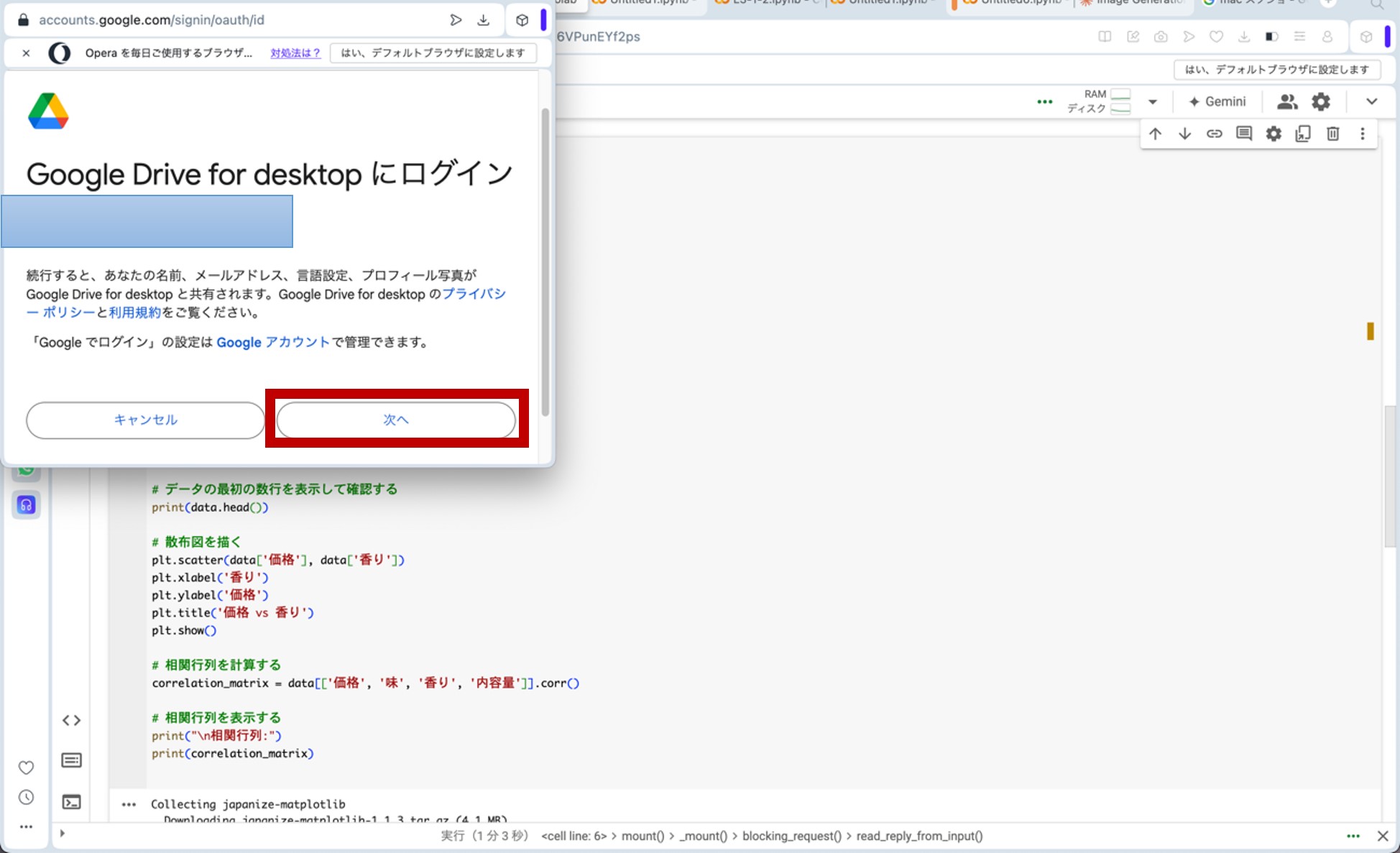
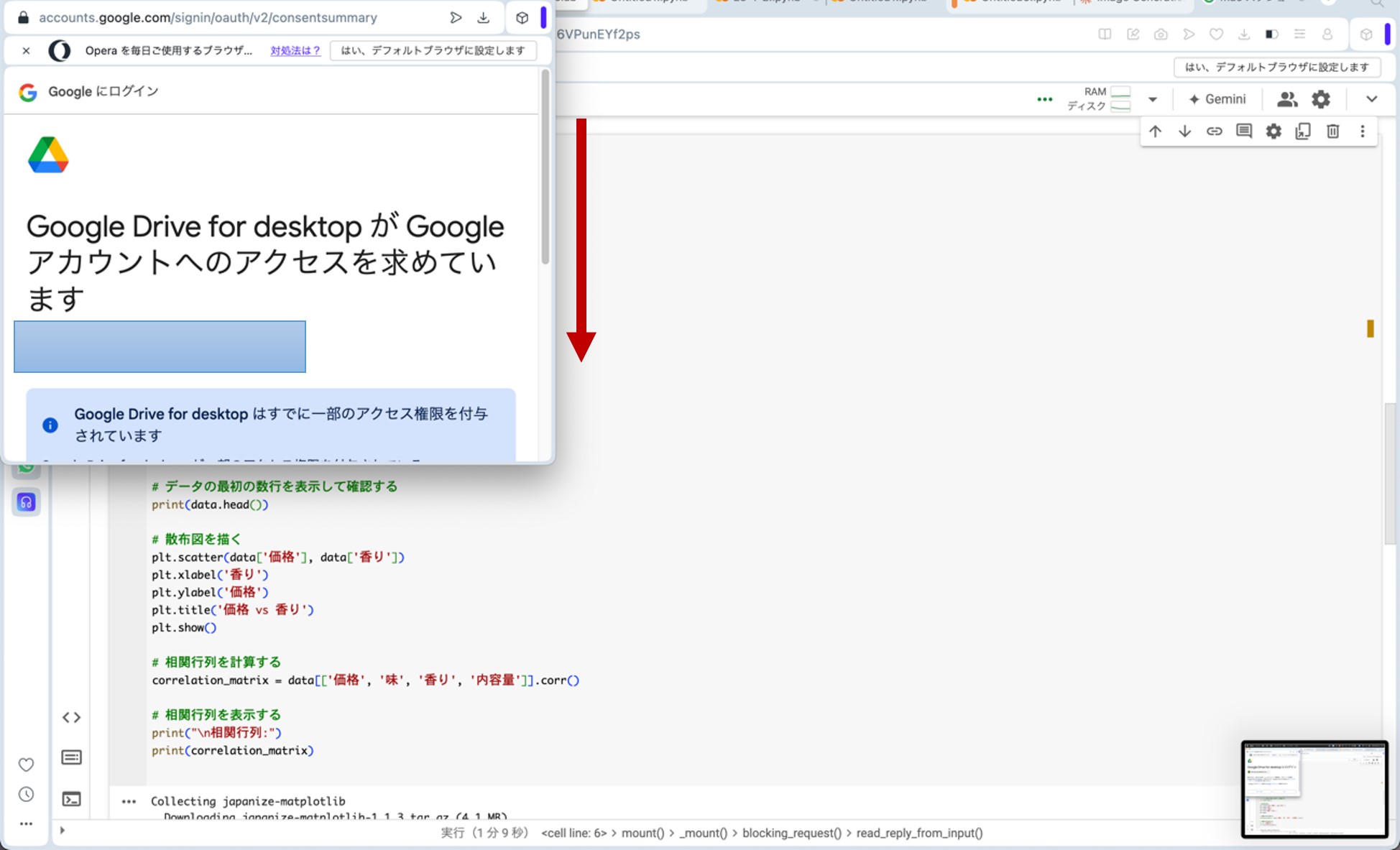
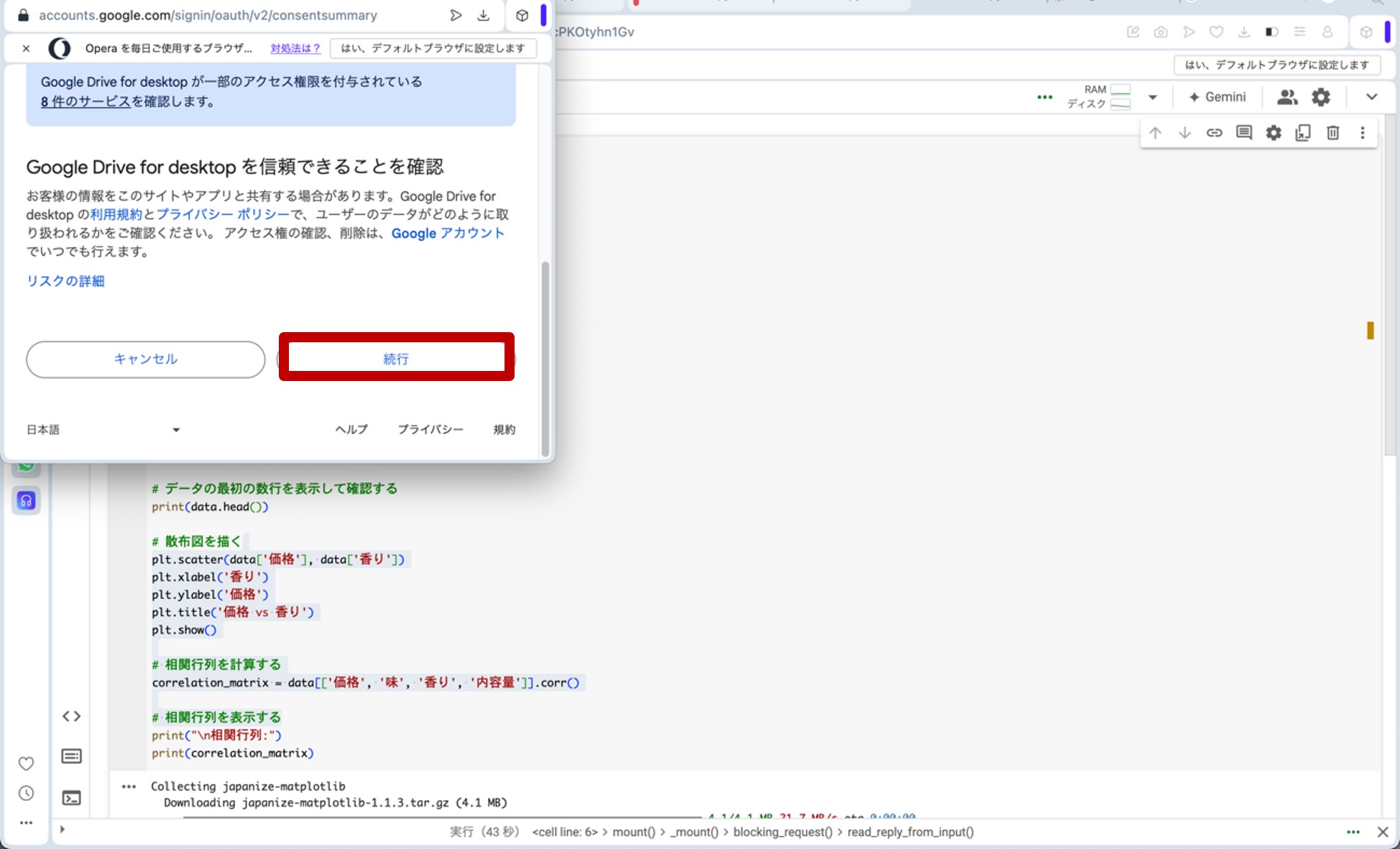
ここで、先ほどのリンクからGoogle Colaboratoryに飛びます。コードセルに以下のプログラムをコピー&ペーストし、コードセル左側にある▷ボタンを押してプログラムを走らせます。途中、ポップアップがいくつか出てきますが、図23の様に進んで下さい(『Googleドライブに接続』をクリック→自分のアカウントを選択→『次へ』をクリック→下へスクロール→『続行』をクリック)。これらの操作によって、先ほどのビールの評価データが生成されます。


図23：ポップアップへの対応

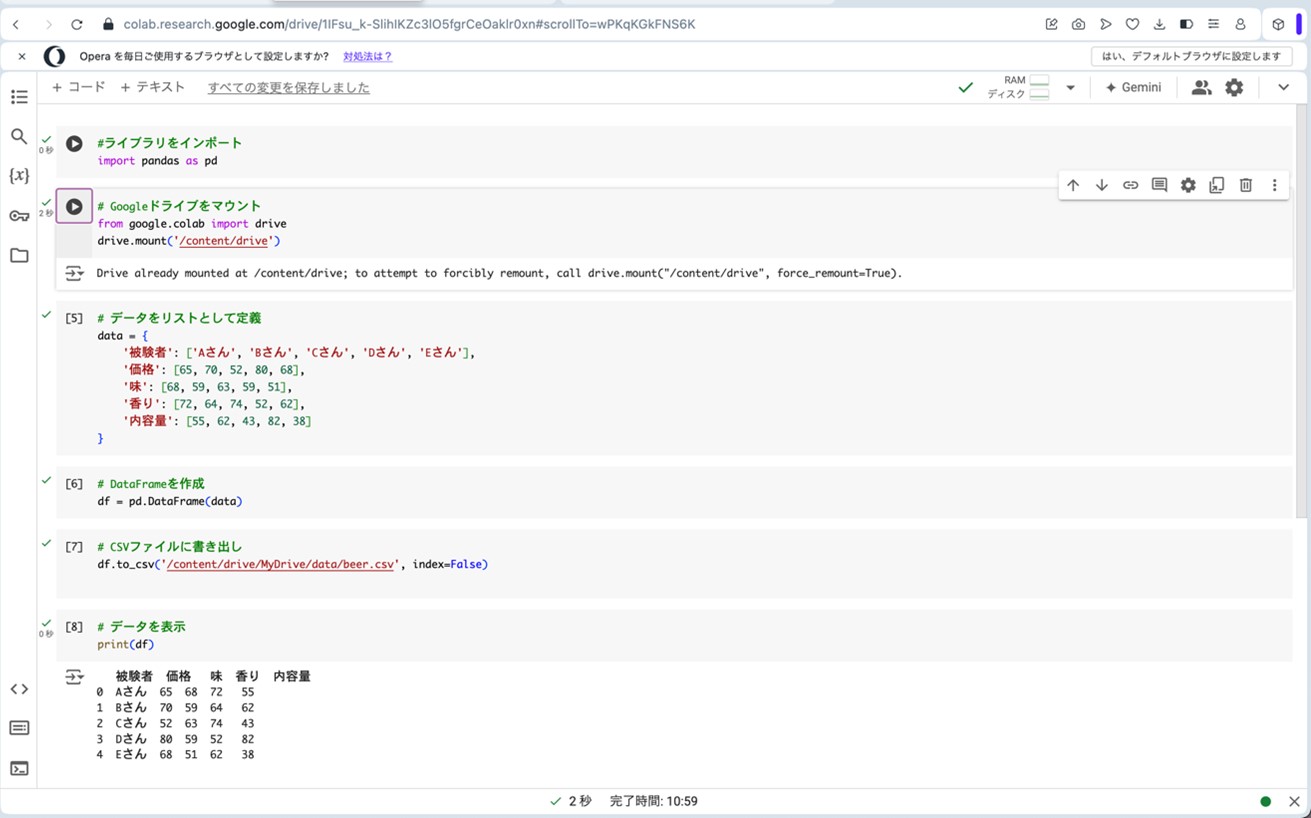
必要なライブラリを読み込みます。ライブラリとは、特定の機能や処理を簡単に使えるようにまとめたプログラムの集まりです。ライブラリをインポートするだけで、複雑な処理を効率的に行えます。ここでは、データ解析用ライブラリであるpandasをインポートします。

================================================================================
#ライブラリをインポート
import pandas as pd
================================================================================

Googleドライブと連携します。

================================================================================
# Googleドライブをマウント
from google.colab import drive
drive.mount('/content/drive')
================================================================================

それぞれの変数を当てはめ、読み込んでいきます。

================================================================================
# データをリストとして定義
data = {
'被験者': ['Aさん', 'Bさん', 'Cさん', 'Dさん', 'Eさん'],
'価格': [65, 70, 52, 80, 68],
'味': [68, 59, 63, 59, 51],
'香り': [72, 64, 74, 52, 62],
'内容量': [55, 62, 43, 82, 38]
}
================================================================================

読み込んだデータを格納します。

================================================================================
# DataFrameを作成
df = pd.DataFrame(data)
================================================================================

格納したデータを、Googleドライブのマイドライブ内の「data」フォルダに「beer.csv」として書き出します。

================================================================================
# CSVファイルに書き出し
df.to_csv('/content/drive/MyDrive/data/beer.csv', index=False)
================================================================================

データを表示します。

================================================================================
# データを表示
print(df)
================================================================================

図24：Google Colaboratoryにプログラムを読み込ませて、ビール評定データを生成

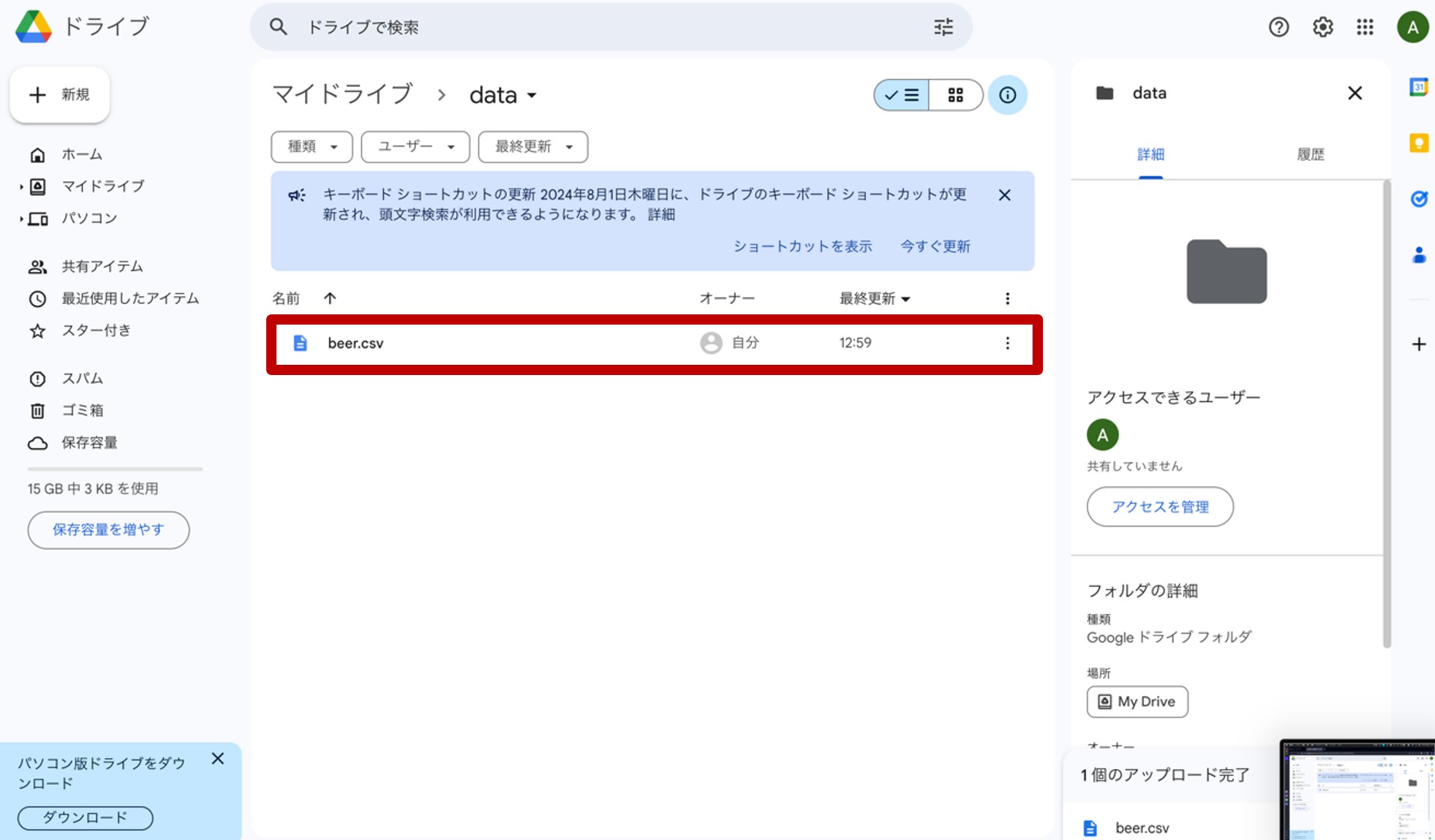
先ほどGoogleドライブのマイドライブ内に作成したdataフォルダをクリックしてみると、beer.csvファイルが格納されているのが確認できます(図25)。

図25：マイドライブの「data」へ「beer.csv」が格納されている

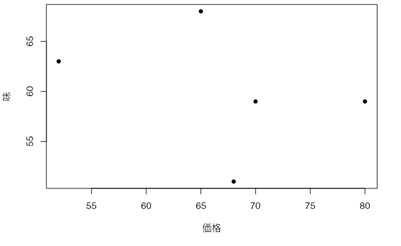
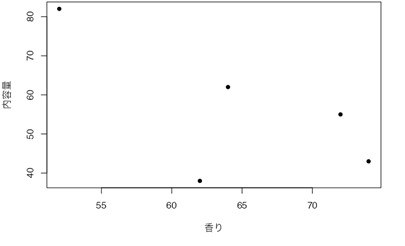
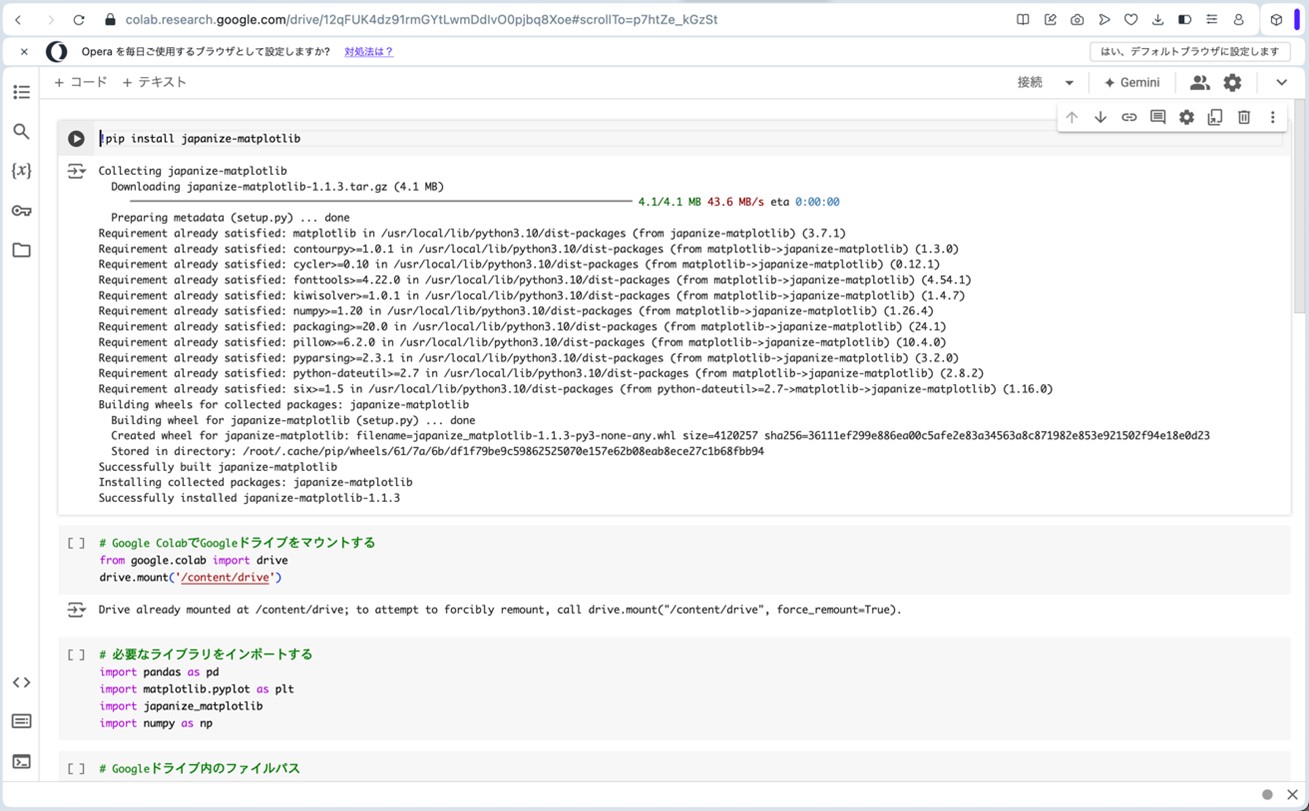
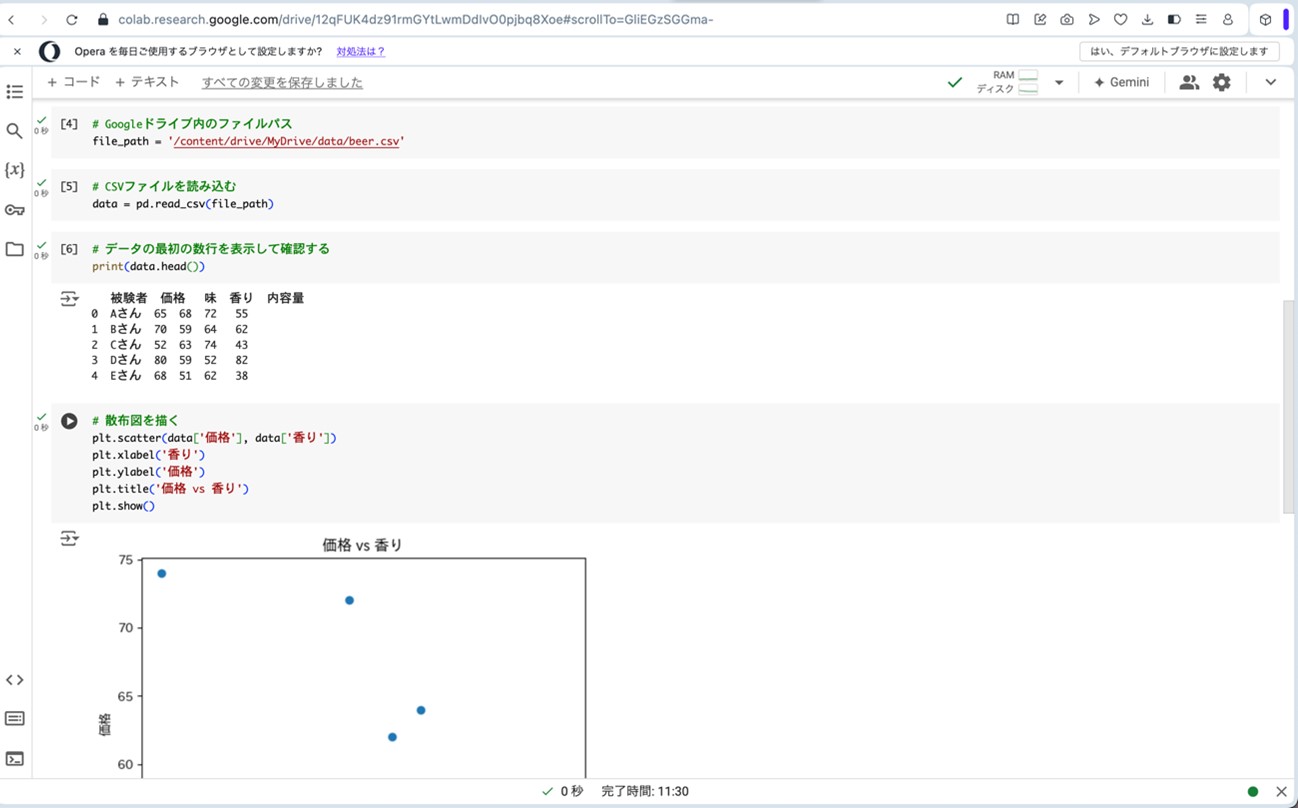
次に、Google Colaboratoryに戻ります。図16〜20の手順を参考に、図21の画面まで進みます。ここで、以下のプログラムをコピーして、コードセルに貼り付けます。そして、▷ボタンを押して、プログラムを走らせると、「価格」と「香り」の散布図と、表３と同様の相関行列が算出されます。

必要なライブラリをインストールします。

================================================================================
!pip install japanize-matplotlib
================================================================================

Googleドライブと連携します。

================================================================================
# Google ColabでGoogleドライブをマウントする
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
# 必要なライブラリをインポートする
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
================================================================================

Googleドライブ内のどこから、どのデータを呼び出すのか指定します。

================================================================================
# Googleドライブ内のファイルパス
file_path = '/content/drive/MyDrive/data/beer.csv'
================================================================================

指定したデータを読み込みます。

================================================================================
# CSVファイルを読み込む
data = pd.read_csv(file_path)
================================================================================

正しくデータが入っているか、最初の数行を表示して確認します。

================================================================================
# データの最初の数行を表示して確認する
print(data.head())
================================================================================

「価格」×「香り」の散布図を出力します。

================================================================================
# 散布図を描く
plt.scatter(data['価格'], data['香り'])
plt.xlabel('香り')
plt.ylabel('価格')
plt.title('価格 vs 香り')
plt.show()
================================================================================

表3の相関行列を計算します。

================================================================================
# 相関行列を計算する
correlation_matrix = data[['価格', '味', '香り', '内容量']].corr()
================================================================================

相関行列を表示します。

================================================================================
# 相関行列を表示する
print("\n相関行列:")
print(correlation_matrix)
================================================================================

図26：サンプルプログラムで相関行列を算出

プログラムは、皆さんが普段使っている言葉と同じようなものです。プログラムを読み込ませることで、コンピューターに司令を出して実行しています。よって、データを他のものに変え、プログラムを少し書き換えれば、様々なデータで相関行列の計算を行うことができます。皆様のお手元のデータで是非お試し下さい。

用語集

1. 変数(数学的意味での)
   変数は、変化する値を表す言葉です。例えば、身長、体重、年齢、気温、売上高などが変数と呼ばれます。
   変数は、大きく2種類に分類されます。
   ・量的変数：数字で表せ、その数字が数値的意味を持つ変数。 (例：身長、体重、年齢、気温、売上高など)
   ・質的変数：カテゴリで表せる変数。ただし、1.男、2.女のように意味はカテゴリですが数字で表すこともあります。 (例：性別、血液型、出身地、商品種別、顧客属性など)
2. 相関関係
   相関関係は、2つの変数がどれだけ関係しているかを表すものです。相関関係には、基本的には、正の相関、負の相関、相関がない、の3種類があります。
   ・正の相関：一方の変数が大きくなるにつれて、もう一方の変数も大きくなる関係。(例: 身長と体重
   ・負の相関：一方の変数が大きくなるにつれて、もう一方の変数は小さくなる関係。(例: ストレスと幸福度
   ・相関がない：2つの変数間に直線的関係が見られない関係。
3. 相関係数
   相関係数は、2つの変数の相関関係の強さを数値で表したものです。相関係数は、-1から1までの範囲の値を取ります。
   ・相関係数=1：完全な正の相関
   ・相関係数=0：相関がない
   ・相関係数 = -1：完全な負の相関
   相関係数の値が大きいほど、相関関係が強いことを意味します。ただし、相関係数はあくまでも相関関係(片方の値が上がれば、もう一方の値も上がること)の強さを示すものであり、因果関係(物事が原因と結果の関係にあること)を示すものではないことに注意する必要があります。

Googleドライブを利用される際はこちらをご確認、ご理解の上ご利用ください。

Google ドライブ利用規約

ドライブにおけるユーザーのプライバシー保護とユーザー自身による管理
Google ドライブ ヘルプ

1. 所属等は執筆当時のもので、現在とは異なる場合があります。
2. また記事中の技術、手法等については、今後の技術の進展、外部環境の変化等によっては、実情と合致しない場合があります。
3. 各記事における最新の動向につきましては、当社までぜひお問い合わせください。

著者プロフィール

プロフェッショナルズストラテジックプランニング局データソリューション部渡邉 成（わたなべ あきら）

この人の書いた記事

• 連載！データ分析①：相関係数

得意領域

• #AI
• #データアナリシス
• #機械学習
• #CX/DX
• #デジタル
• #効果検証

著者について詳しく見る