データサイエンス 統計学 データ分析 機械学習 AI マーケティング 2025.02.18
連載！データ分析②：回帰分析

回帰分析とは何か？基本から学ぶデータ分析の第一歩

データの背後に潜むパターンや関係性を明らかにするための分析手法の一つに、「回帰分析」があります。これは、ある変数（目的変数：予測したい値）が別の変数（説明変数：目的変数に影響を与える要因の値）によって、どのように影響を受けるのかを数値的に捉える方法です。たとえば、「気温が上がるとアイスクリームの売り上げが増える」という直感的な関係性を数式として表し、その強さや正確さを評価することが可能です。これにより、ただの観察に留まらず、将来の予測や意思決定の基盤を築くことができます。
回帰分析は、マーケティングや経済学、心理学、工学など、幅広い分野で応用されています。たとえば、商品の価格設定が売り上げに与える影響を調べたり、健康診断のデータから病気のリスクを予測したりする場面で活用されます。このように、回帰分析は私たちの日常生活やビジネスの場面で重要な役割を果たしているのです。
本記事では、回帰分析の基本的な考え方や種類、実際の手法について、初心者の方にも分かりやすく解説していきます。分析の第一歩として、ぜひ回帰分析の魅力に触れてみてください。

単回帰分析とは？その基本と仕組みを理解しよう

単回帰分析は、回帰分析の中でも最も基本的な手法であり、1つの説明変数を使って1つの目的変数を予測するものです。データ分析初心者でも取り組みやすいこの手法は、関係性をシンプルに捉えることができるため、統計学やデータサイエンスの学びの第一歩としても最適です。本章では、単回帰分析の基本的な仕組みとその使い方を詳しく解説します。

単回帰分析の基本構造

単回帰分析では、次のような関係性を数式で表します。

y=a+bx+ε

ここでの各項の意味を見ていきましょう。

1. y：目的変数（予測したい値）
2. x：説明変数（目的変数に影響を与える要因）
3. a：切片（説明変数が0のときの目的変数の値）
4. b：回帰係数（各説明変数が目的変数に与える影響の強さ。説明変数が1単位増えると、目的変数がどれだけ増減するかを示す）
5. ε：誤差項（モデルが説明しきれない部分）

例えば、「勉強時間（説明変数）」が「試験の点数（目的変数）」に与える影響を調べる場合、上記の式でその関係性を表します。この式を使うことで、「勉強時間が1時間増えると点数が何点上がるか」を具体的に計算できます。具体的には、bが10という結果が出た場合、「勉強時間が1時間増えると点数は10点上がる」と解釈できます。
図示すると以下のようになります。青のドットがデータ、赤のラインが単回帰分析の直線です。要するに、中学校の時に習った1次関数ですね。

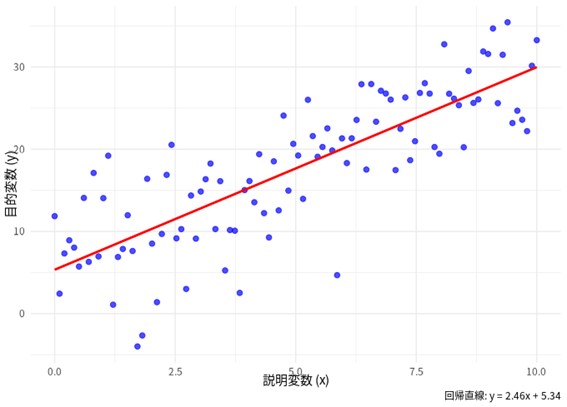
回帰係数の意味と解釈

単回帰分析の結果として得られる回帰係数（b）は、説明変数が目的変数に与える影響を具体的に示します。回帰係数が「2」であれば、説明変数が1単位増加すると目的変数が2増えることを意味します。また、回帰係数の符号（プラスかマイナスか）は、関係性が正の相関なのか負の相関なのかを表します(片方の変数の値が増えるともう一方の変数の値も増えるのか、または片方の変数の値が増えるともう一方の変数の値が減るのかを表します)。
一方、切片（a）は、説明変数が0のときに目的変数がどの値を取るかを示します。たとえば、勉強時間が0のときの試験の点数が切片として表されます。

決定係数（R2）とｐ値でモデルの精度を確認

(単回帰分析でも後述する重回帰分析でも)回帰分析の結果が良いかどうかを判断するための重要な指標が決定係数（R2）です。これは、目的変数の変動のうち何割が説明変数で説明されているかを示します。
例えば、R2=0.8であれば、「データの80%が説明変数で説明されている」と解釈できます。
値が1に近いほどモデルの当てはまりが良いことを意味しますが、過剰に高い場合はデータの偏り等の可能性も考慮しましょう。
また、モデルの精度を確認するもう一つの手段としてp値があります。p値とは、説明変数が統計的に意味があるかどうかを判断する指標です。言い換えれば、「偶然ある事象が起こる確率」のことです。数字が小さいほど、「偶然では説明できない差がある」と判断します。基準としては、p値が0.05未満なら「意味のある結果」とみなすことが多いです。

重回帰分析とは？複数の要因を考慮したデータ分析の基本

重回帰分析は、複数の説明変数を用いて1つの目的変数を予測する回帰分析の手法です。単回帰分析が「1対1」のシンプルな関係を捉えるのに対し、重回帰分析では複数の要因が絡み合った複雑な現象を数式で表現します。現実世界では、ある結果が1つの要因だけで決まることは少ないため、重回帰分析は非常に実用性が高い手法といえます。本章では、重回帰分析の仕組みやその活用方法について解説します。

重回帰分析の基本構造

重回帰分析では、次のような方程式を用います。

y=a+b1x1+b2x2+⋯+bnxn+ε

この式の各項の意味を整理します。

1. y：目的変数（予測したい値）
2. x1,x2,⋯ ,xn：説明変数（目的変数に影響を与える要因）
3. a：切片（全ての説明変数が0のときの目的変数の値）
4. b1,b2,⋯ ,bn：回帰係数（各説明変数が目的変数に与える影響の強さ。説明変数が1単位増えると、目的変数がどれだけ増減するかを示す）
5. ε：誤差項（モデルが説明しきれない部分）

例えば、「家賃（目的変数）」を予測する場合、説明変数として「部屋の広さ」「駅からの距離」「築年数」などを考慮できます。重回帰分析では、これら複数の要因が家賃にどのような影響を与えるかを数値的に示すことが可能です。
図示すると以下のようになります。青いドットがデータ、オレンジの平面が重回帰分析の平面です(この場合、目的変数1つ、説明変数2つの3次元で表すので直線ではなく平面になります)。

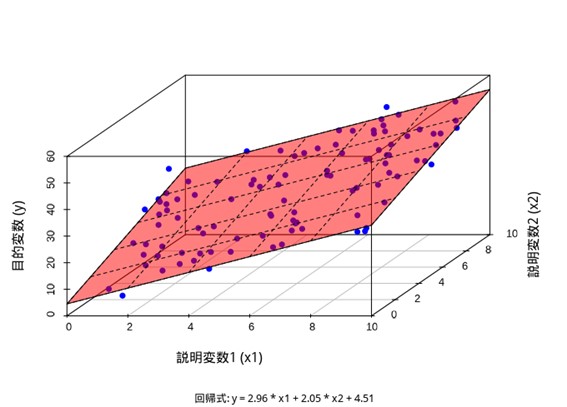
直感的には少々分かりにくいかもしれませんね。次項で具体例を見ていきましょう。

回帰係数の解釈

重回帰分析の結果として得られる回帰係数（b1,b2,⋯ ,bn）は、各説明変数が目的変数に与える影響を示します。ただし、重回帰分析では他の説明変数の影響を考慮している点が単回帰分析と異なります。
例えば、以下のような結果が得られたとします。

y=50+3x1-2x2-0.2x3

ここで、

1. y：「家賃（円）」
2. x1：「部屋の広さ（㎡）」
3. x2：「駅からの距離（分）」
4. x3：「築年数（年）」

この場合、

1. b1=3：部屋の広さが1㎡増えると、家賃が3万円上がる。
2. b2=-2：駅からの距離が1分遠くなると、家賃が2万円下がる。
3. b3=-0.2：築年数が1年増えると、家賃が0.2万円下がる（逆に、築年数が多いほど家賃が安い）。

他の変数の影響を一定とした上での影響度が数値化されるため、より現実に即した解釈が可能です。

多重共線性のリスクと対策

重回帰分析を行う際の注意点の一つが「多重共線性」です。これは、説明変数同士が強い相関関係を持つ場合に生じる問題で、以下の影響を与えます。

1. 回帰係数の信頼性が低下する(回帰係数の結果が当てにならなくなる)。
2. 解析結果が不安定になり、予測精度が下がる。

多重共線性の有無は、VIF（Variance Inflation Factor：分散膨張係数）という指標を用いて確認します。一般的に、VIFが10を超える場合、多重共線性が強いとされます。

決定係数（R2）とｐ値でモデルの精度を確認

重回帰分析の結果を評価するためには、以下の指標を確認します。
決定係数（R2）：目的変数の変動をどの程度説明変数が説明できているかを示す。値が1に近いほどモデルの当てはまりが良い。

1. p値：各説明変数が統計的に意味があるかどうかを判断する指標。

これらの指標を活用することで、モデルの信頼性を高め、より正確な予測が可能となります。

標準化偏回帰係数を用いた重回帰分析とは？

説明変数の単位が異なる場合、回帰係数の値だけでは説明変数の影響力を直接比較するのが難しいことがあります。この問題を解決するために使用されるのが「標準化偏回帰係数β」(回帰係数ｂの別バージョン)を用いた重回帰分析です。方程式は以下のようになり、重回帰分析のbをβに変えただけで基本構造は先ほどの重回帰分析と同じです。

y=a+β1x1+β2x2+⋯+βnxn+ε

この式の各項の意味を整理します。

1. y：目的変数（予測したい値）
2. x1,x2,⋯ ,xn：説明変数（目的変数に影響を与える要因）
3. a：切片（全ての説明変数が0のときの目的変数の値）
4. β1,β2,⋯ ,βn：標準化偏回帰係数（各説明変数が目的変数に与える影響の強さ）
5. ε：誤差項（モデルが説明しきれない部分）

標準化偏回帰係数の解釈

標準化偏回帰係数βは、全ての変数を標準化（平均0、標準偏差1、-1〜1の間の値に変換すること）した上で計算されるため、単位に左右されずに各説明変数の目的変数への相対的な影響力を比較することが可能です。

1. y：「家賃（円）」
2. 値が大きいほど、目的変数に対する影響力が強いことを示します。
3. 符号は、回帰係数と同様に正負の関係を表します。

たとえば、以下のような標準化偏回帰係数が得られた場合：

1. y：「家賃（円）」
2. x1「部屋の広さ」：β1=0.6
3. x2「駅からの距離」：β2=-0.4
4. x3「築年数」：β3=-0.2

この結果から、部屋の広さが目的変数に最も強い影響を与えており、駅からの距離と築年数は負の影響を与えていることがわかります。

分析環境の構築

さて、本連載の最後には、Pythonというプログラム言語を使ってデータ分析をする方法が記載されています。それには事前準備(環境構築)が必要です。

プログラムを動かすために使用するのが、Google社の提供する、Google Colaboratory とGoogleドライブです。具体的には、Google Colaboratory 上でプログラムを動かして、Googleドライブに格納したデータを呼び出して分析する、という仕組みになっています。

以下に、その事前準備の方法を解説していきます。

Googleドライブ

まずは、Googleドライブからです。Googleのアカウントを持っている人はサインイン、Googleのアカウントを持っていない人はアカウントを作成(サインアップ)し、上記のリンクからGoogleドライブに飛んで下さい。すると、図3のようなホーム画面が出てきます。

図3.Googleドライブのホーム画面

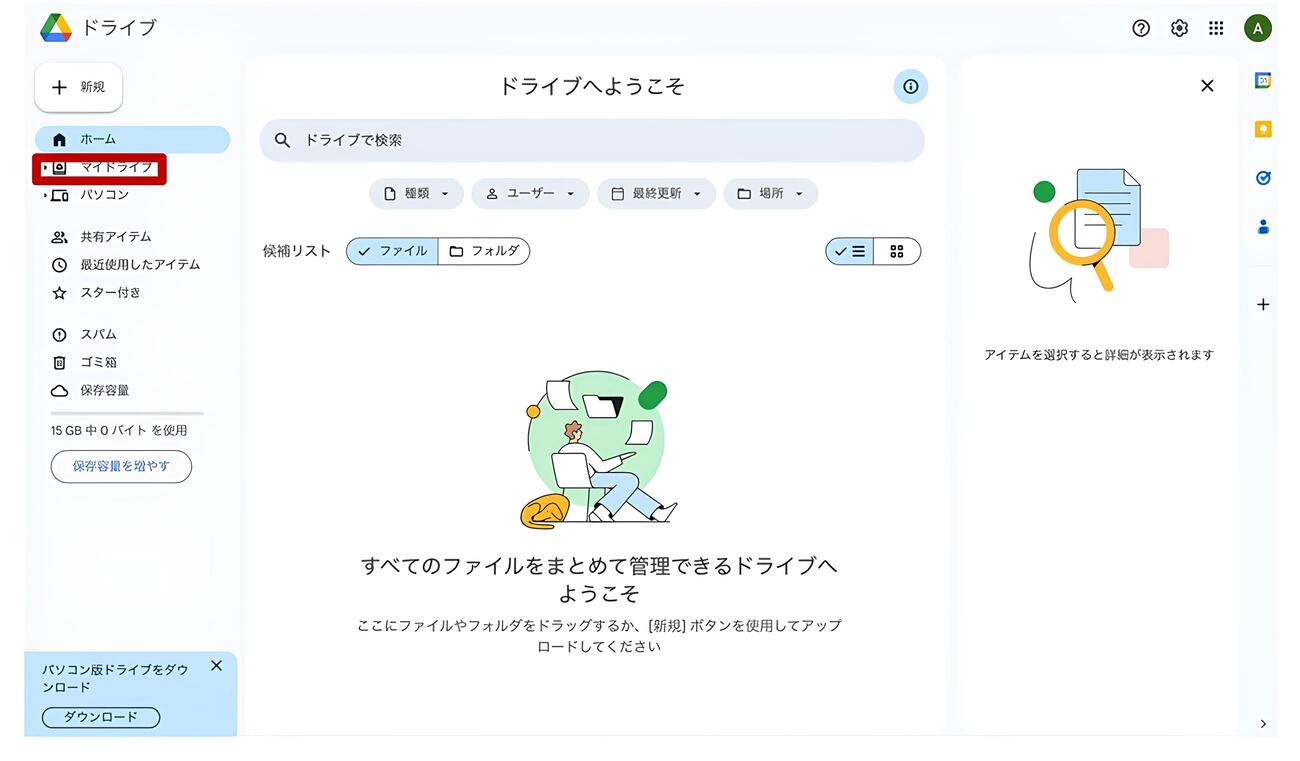
左上の『マイドライブ』をクリックすると、図4のような画面が現れます。自分で入れたファイルはまだありませんが、ここに、これからの連載ごとに使用するデータを格納していきます。

図4.マイドライブの中身

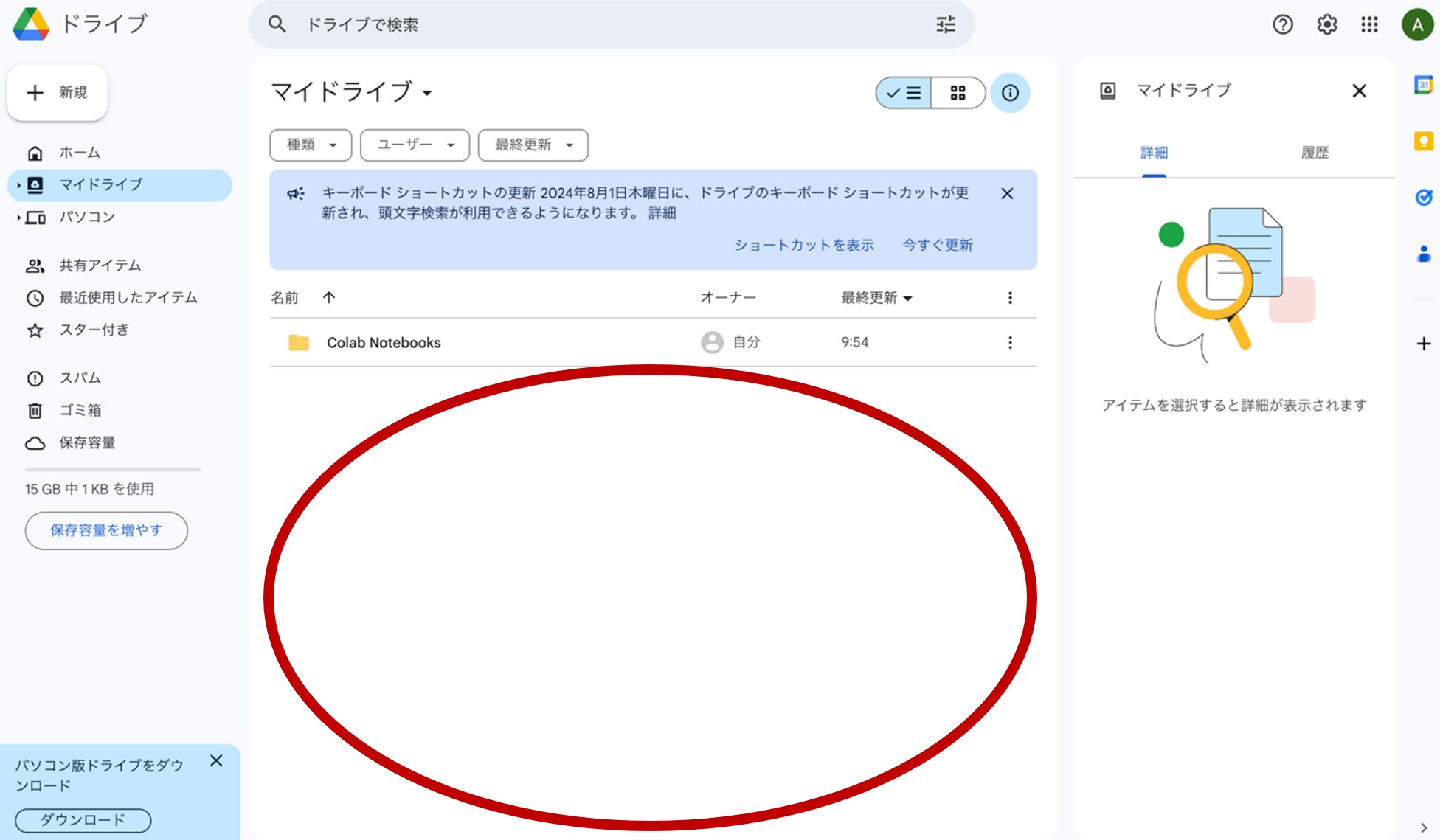
画面中央下の空白(図4の赤丸部分)を右クリックして下さい。すると図5のような表示が現れます。ここから、Google Colaboratoryの設定をしていきます。

図5.Google Colaboratoryを追加

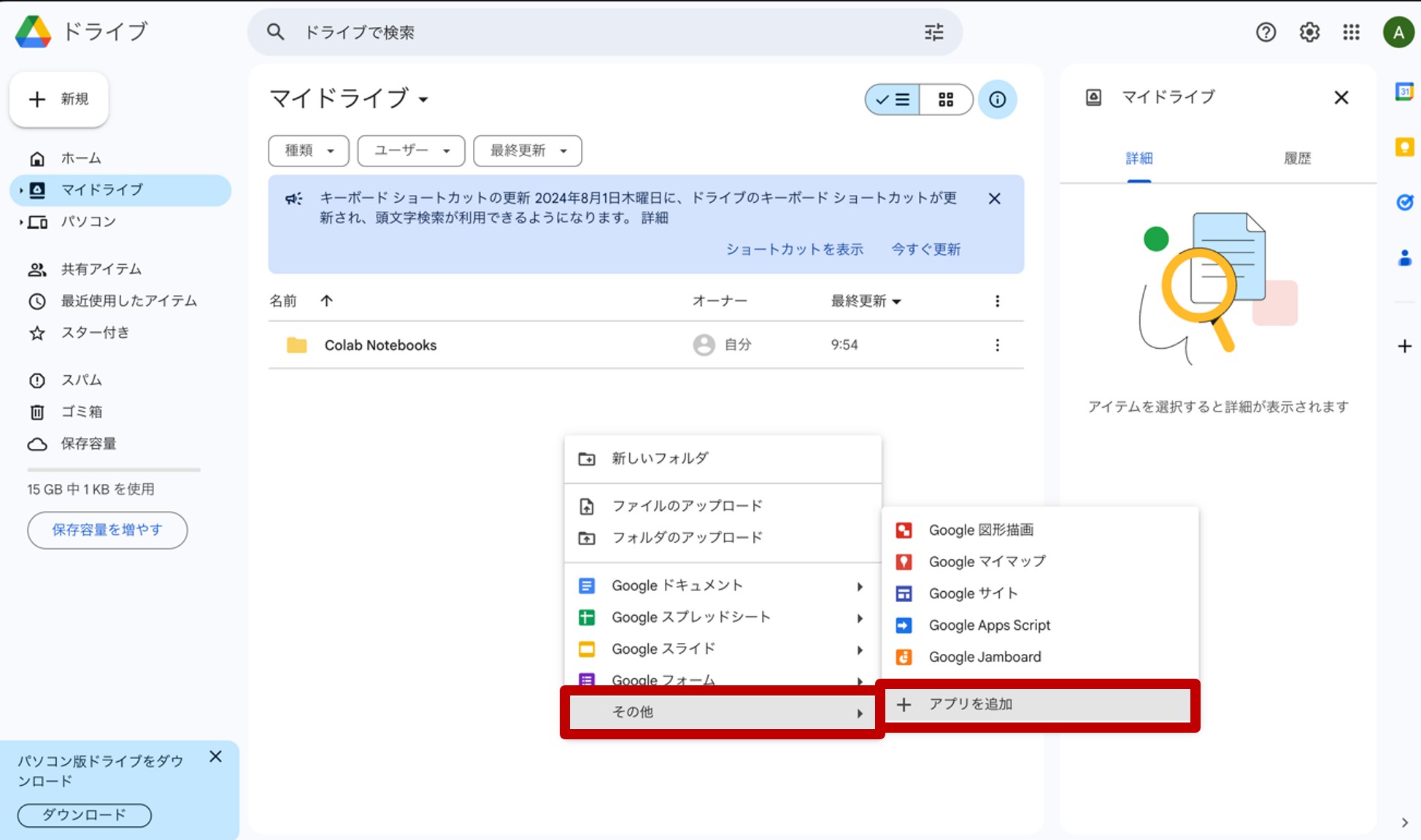
ここで、『その他』→『アプリを追加』をクリックします。

図6.Google Colaboratoryをインストール

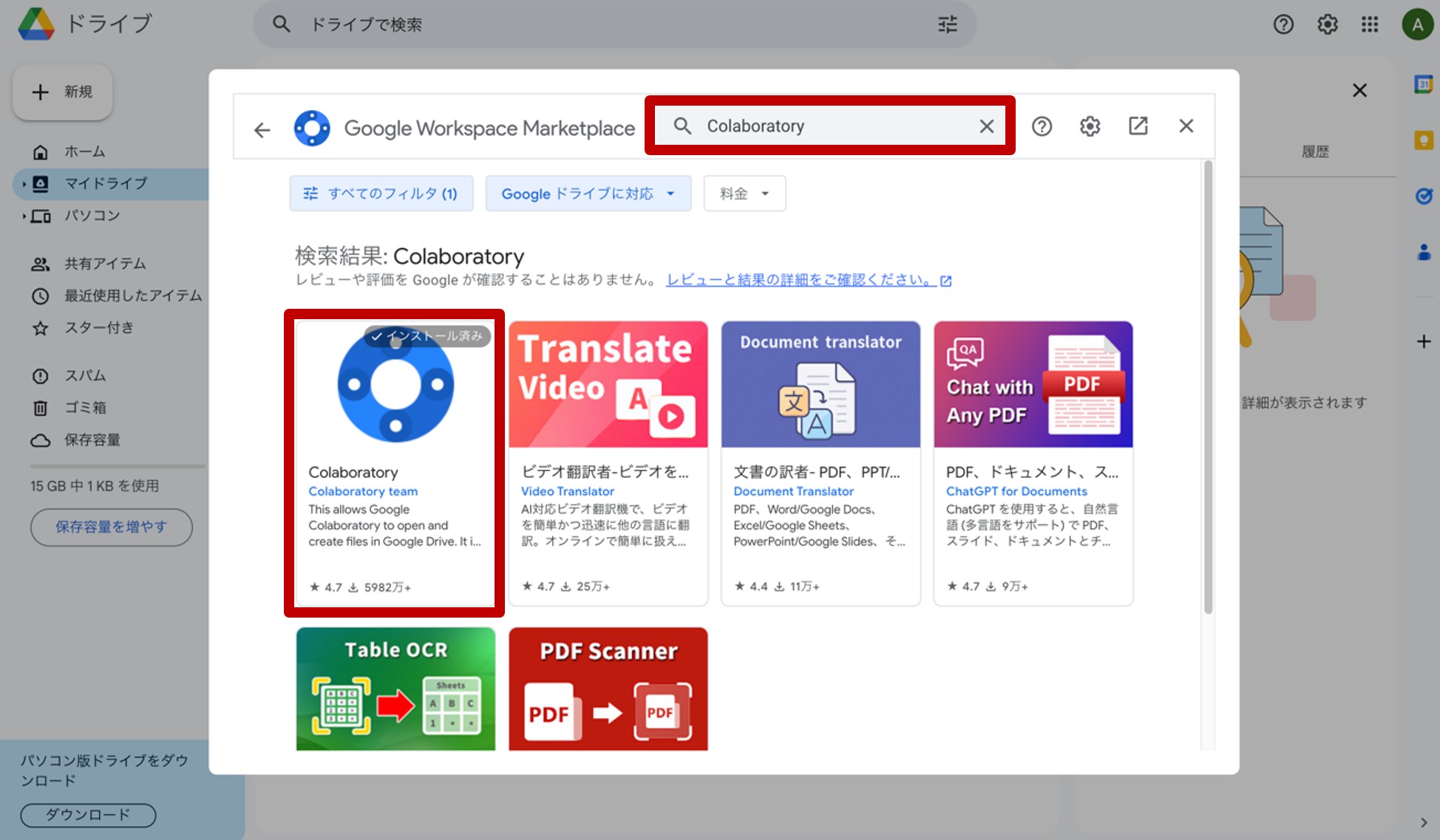
現れた画面の検索窓に『Colaboratory』と入力して検索し、インストールして下さい(図19)。以上で、Googleドライブ上での下準備は終了です。

Google Colaboratory

次に、Google Colaboratoryです。上記のリンクから飛ぶと、図7の様なホーム画面が現れます。

図7.Google Colaboratoryのホーム画面

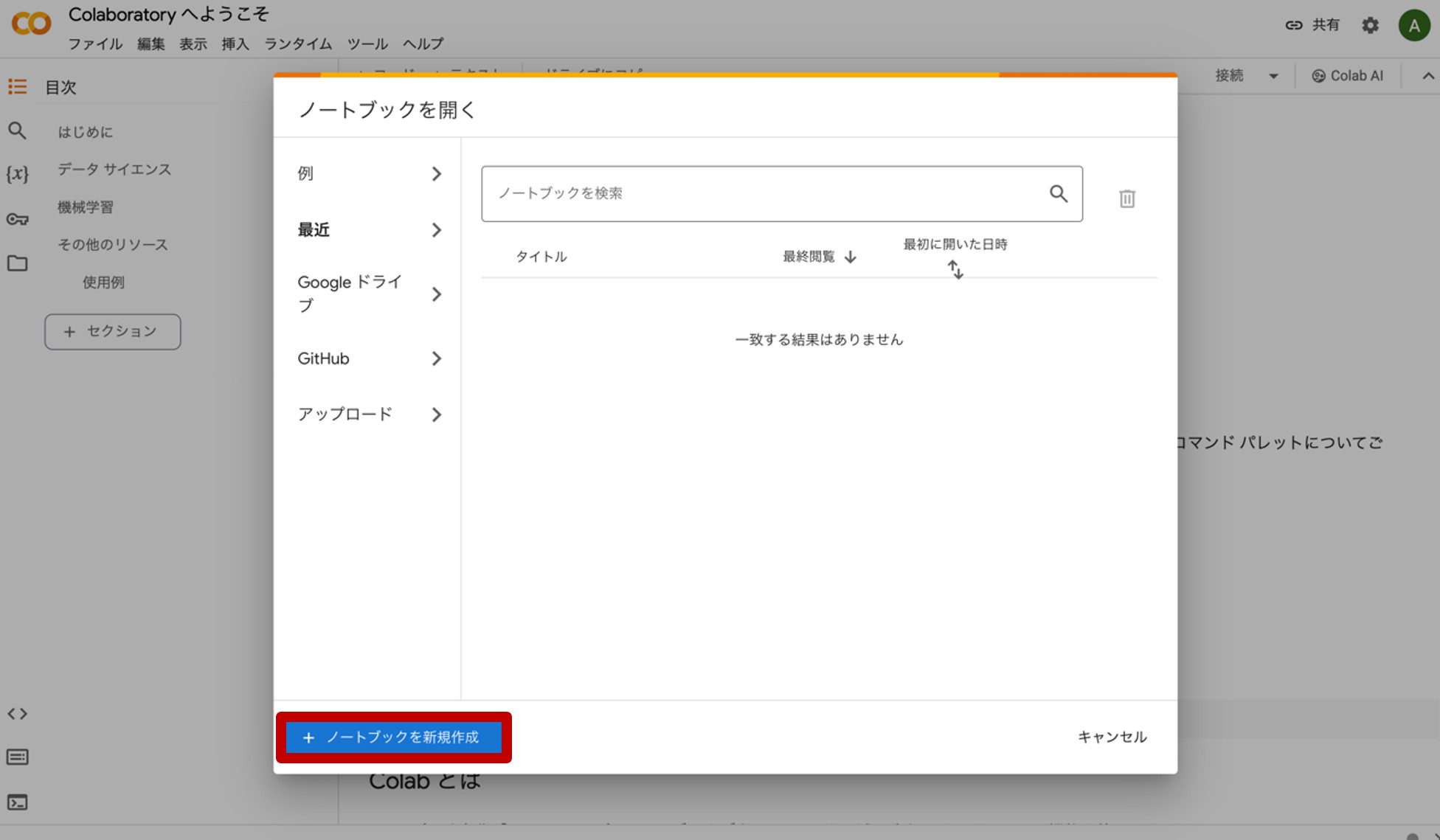
画面下側にある『ノートブックを新規作成』をクリックすると、図8のような画面が現れます。

図8.Google Colaboratoryのプログラムとテキスト入力画面

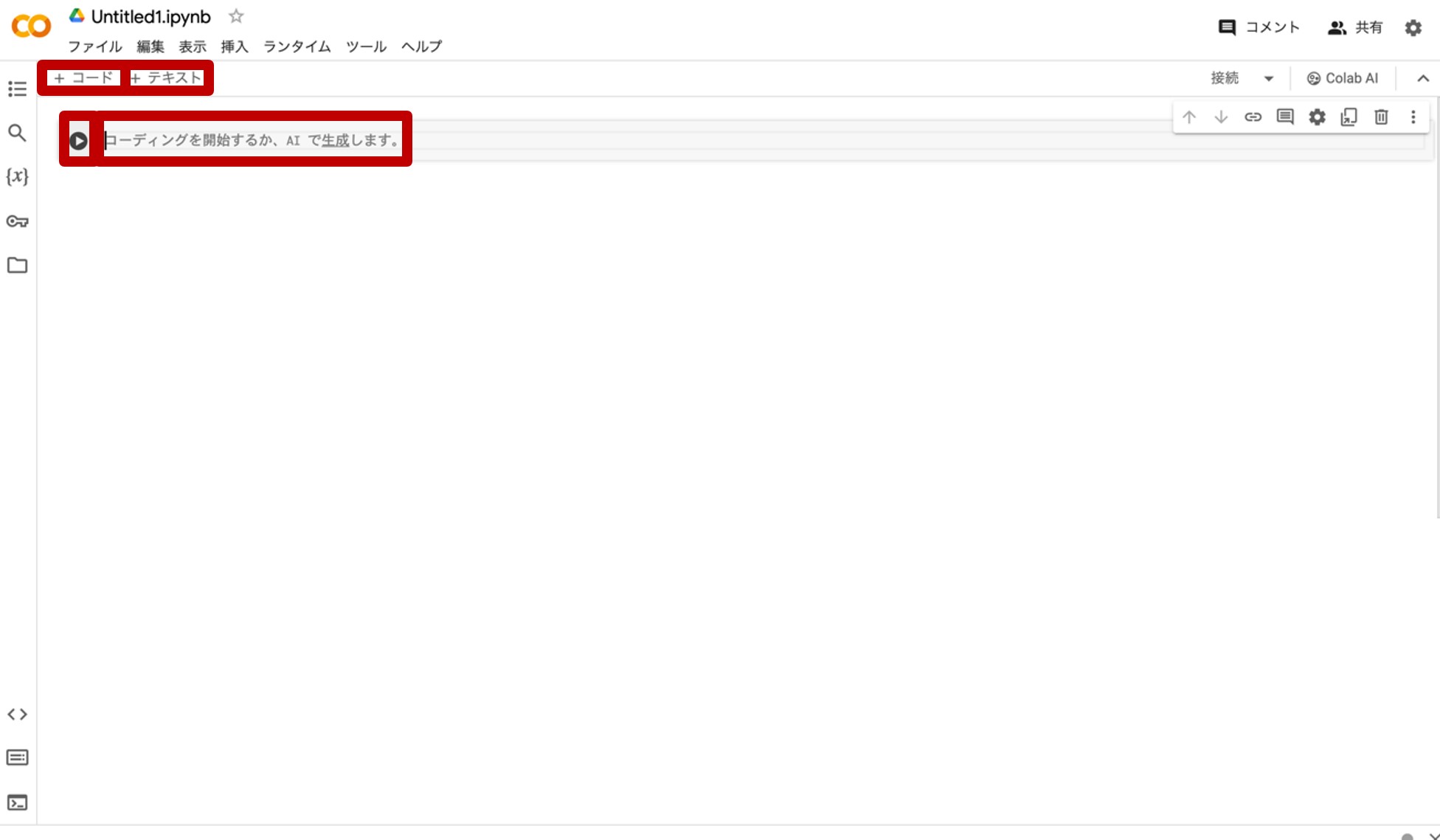
『コーディングを開始するか、AIで生成します。』(AI生成については本連載では省略します。)とあるのが、プログラムを書き込む場所であるコードセルです。左の▷ボタンを押すと当該プログラムが走り出します。分割してプログラムを書きたいときは、その上の『+コード』をクリックするとコードセルを追加することができます。
次に、『+テキスト』をクリックすると出現するのが、コードセルにあるプログラムの解説やメモを書くことができる「テキストセル」です。
以上で下準備は終了です。ここで構築した分析環境を、各連載のデモ分析の際に役立てて下さい。

実際のデータとPythonのプログラム

以下に、Pythonを用いて架空のデータを生成する方法と、重回帰分析を実行するPythonのプログラムを用意しています。
実際にみなさんのお手元のPCで計算して、実際の分析がどのような感覚か、まずは直感的に味わってみましょう(プログラムの文法等はひとまず置いておきましょう。)。
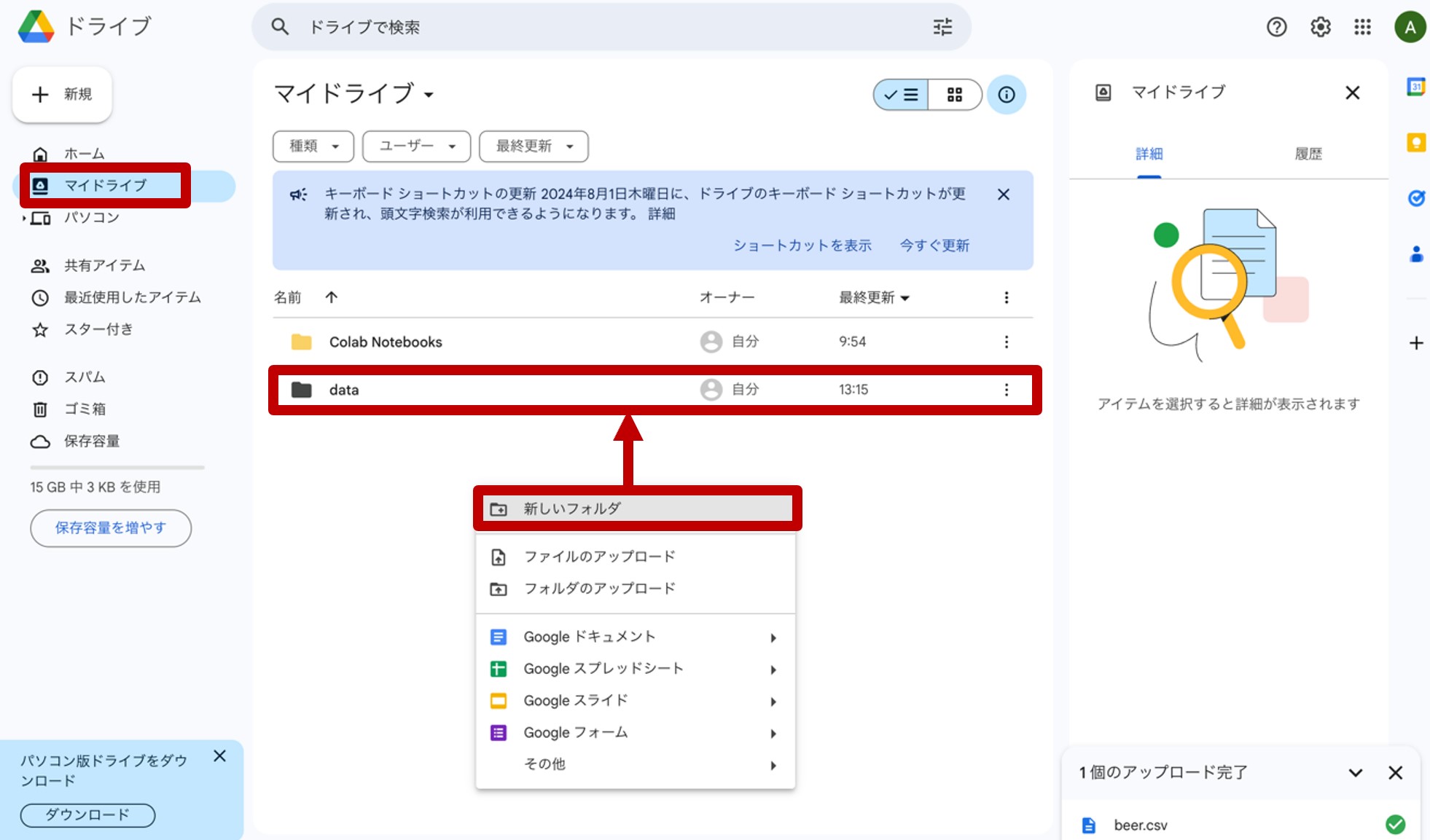
先ほどのリンクからGoogleドライブに飛び、『マイドライブ』を開きます。『マイドライブ』の空白部分を右クリックして『新しいフォルダ』を開き、「data」という名称のフォルダを作成します。(図9)

図9.マイドライブに「data」フォルダを作成

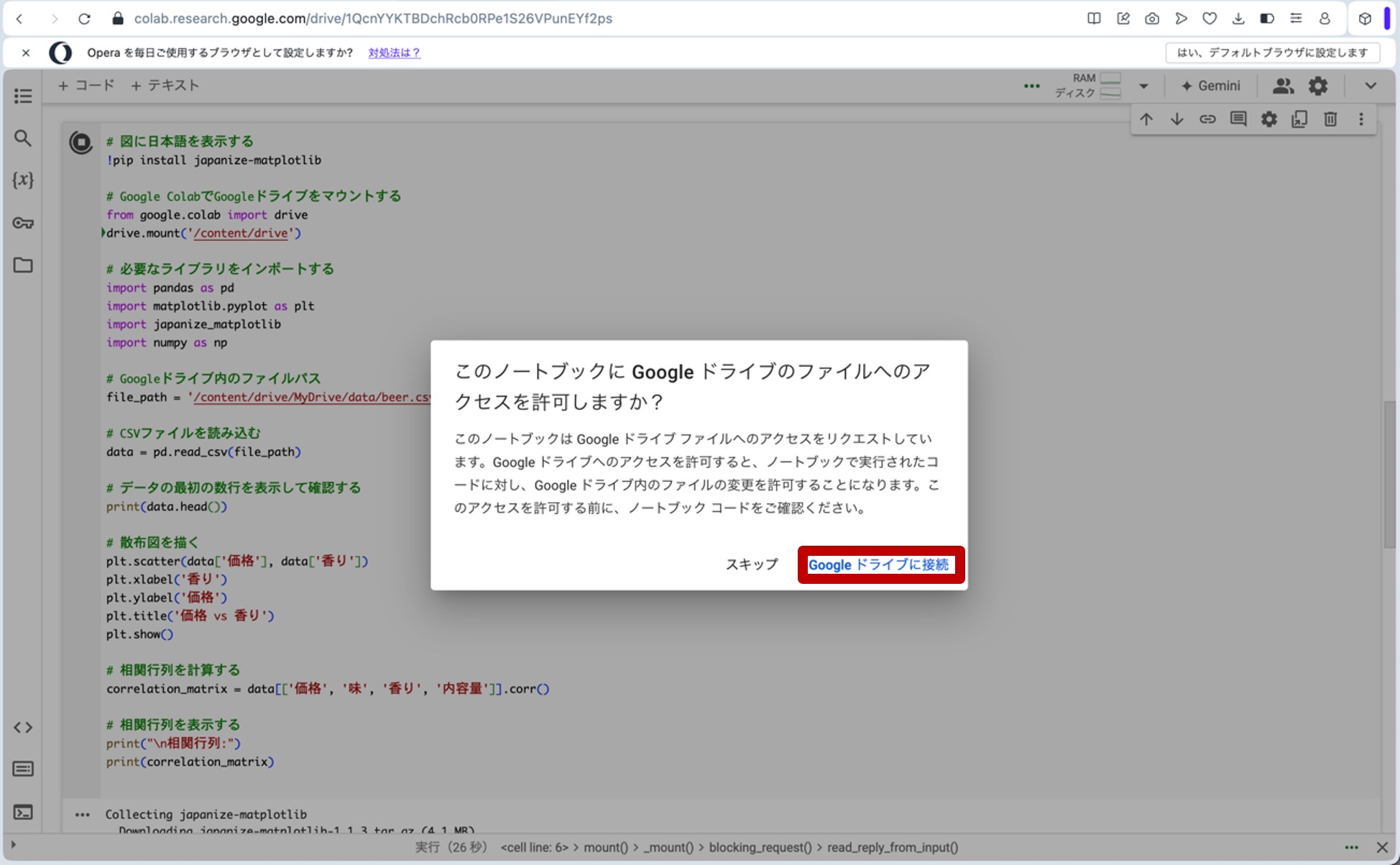
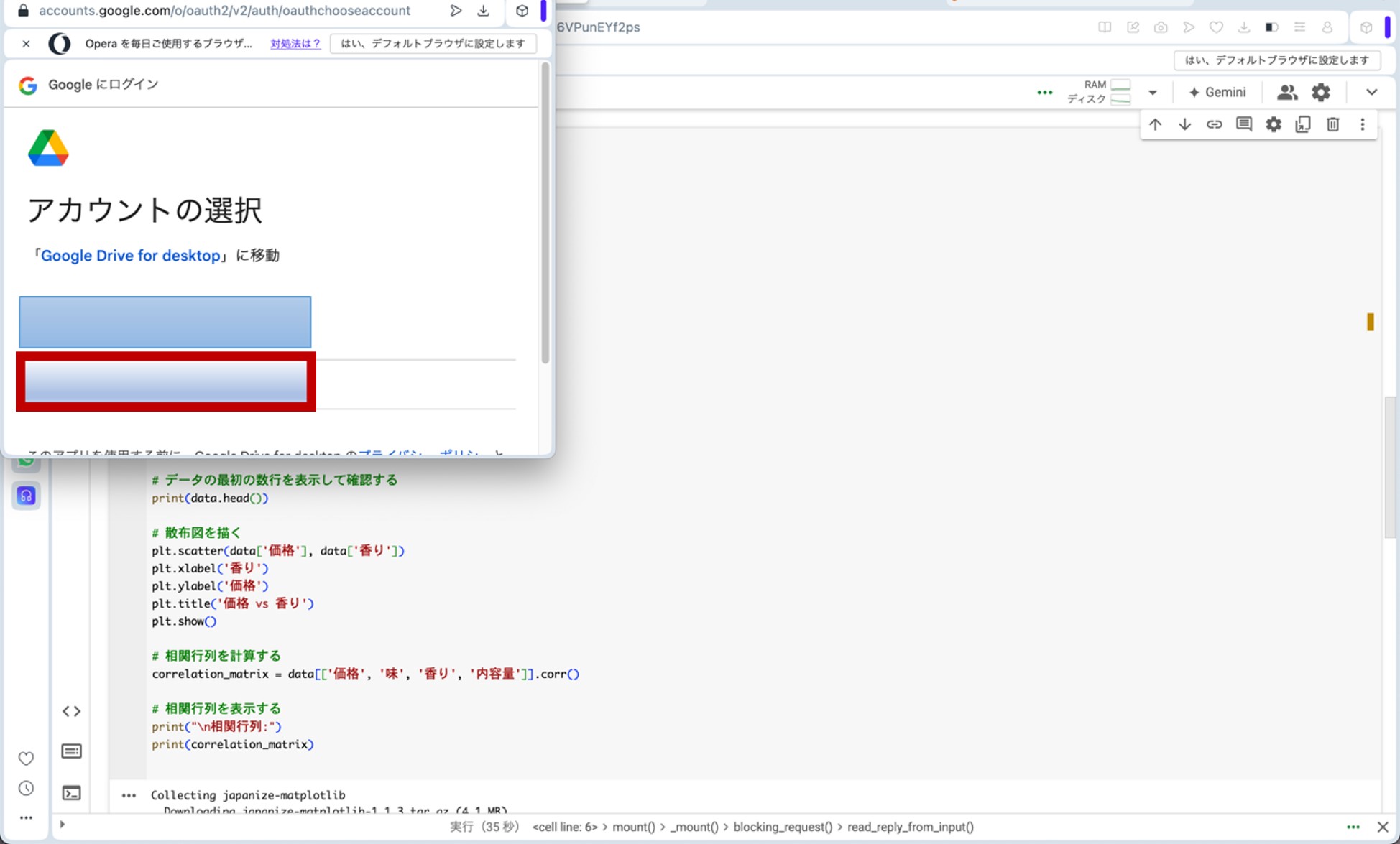
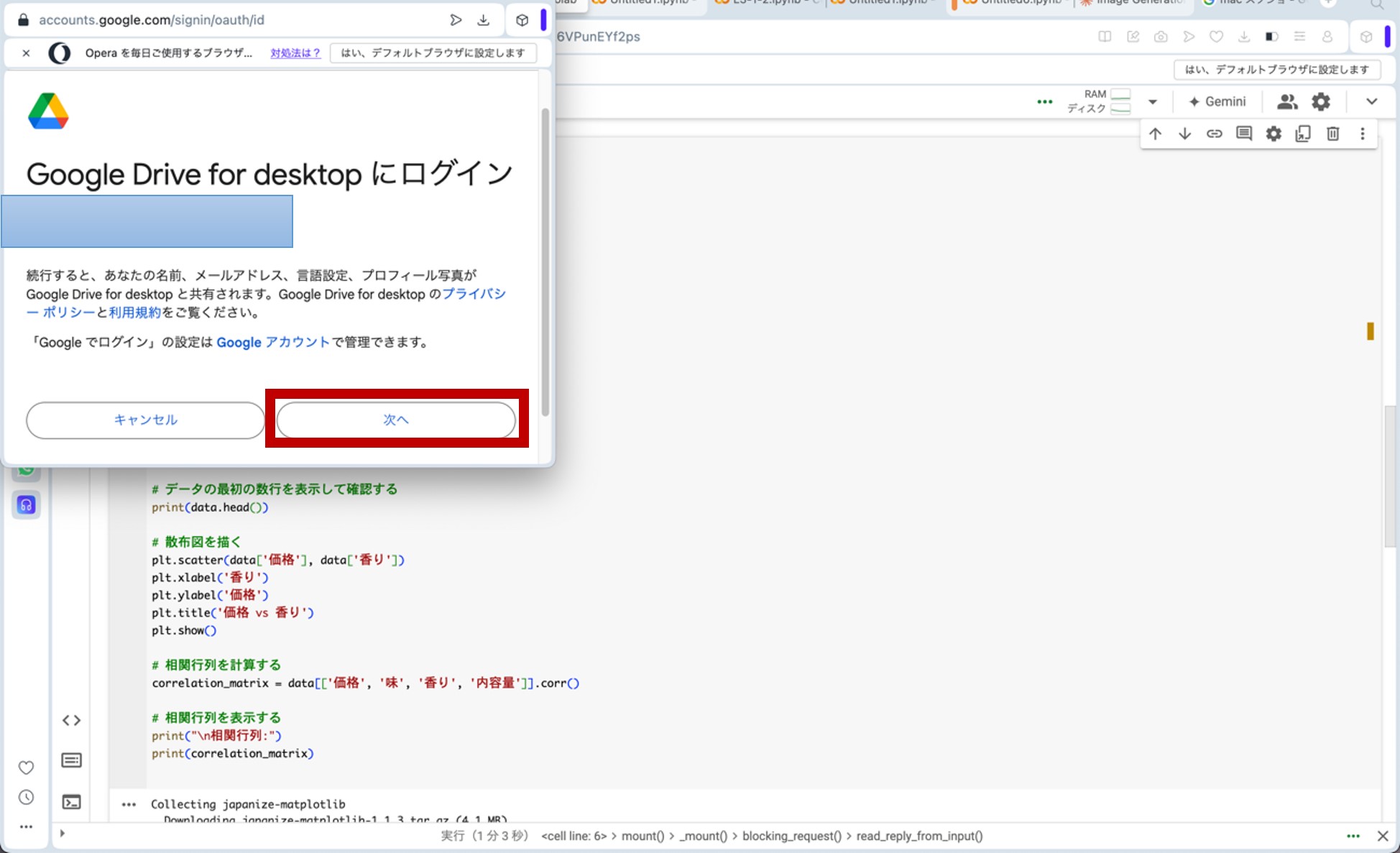
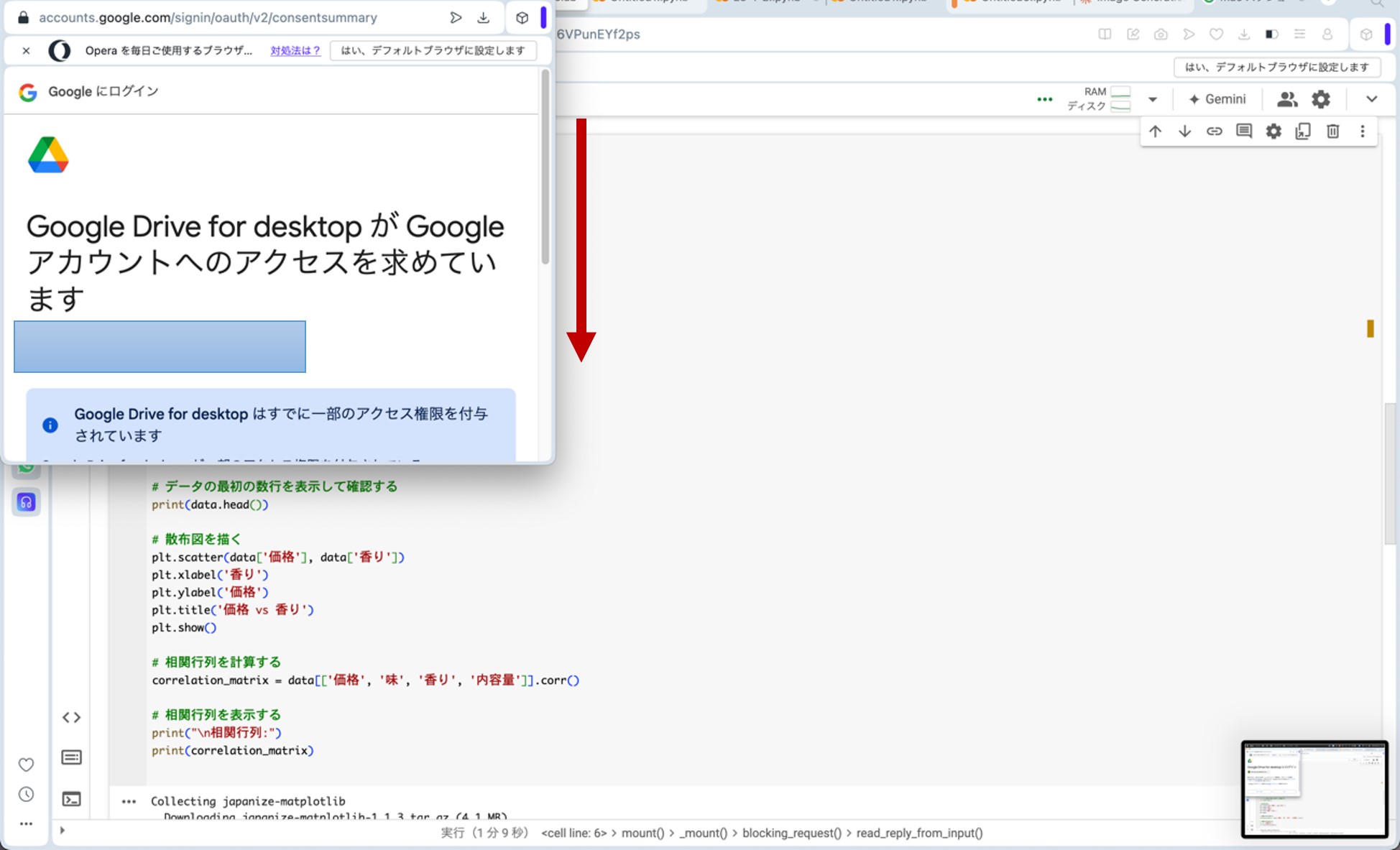
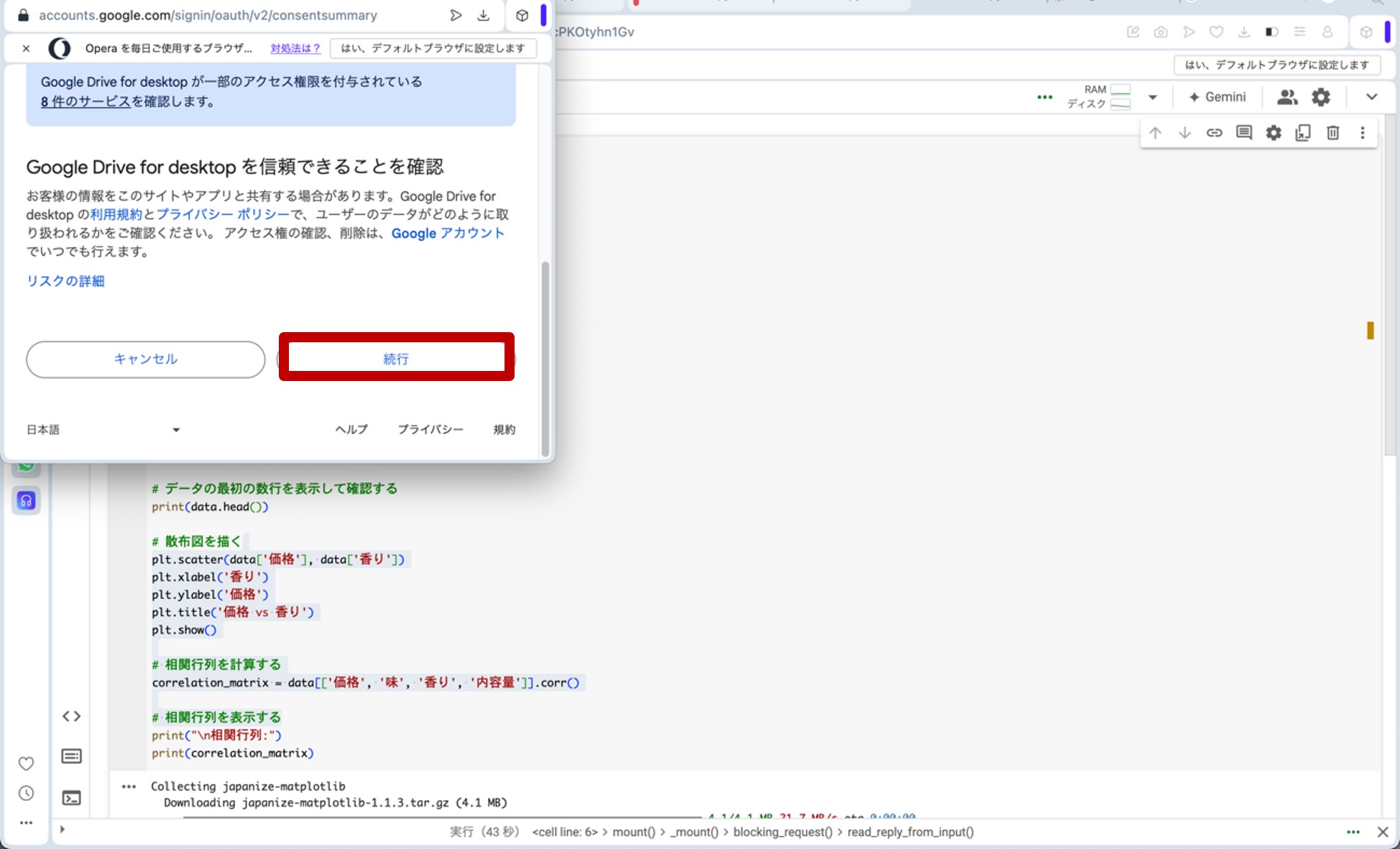
ここで、先ほどのリンクからGoogle Colaboratoryに飛びます。コードセルに以下のプログラムをコピー&ペーストし、コードセル左側にある▷ボタンを押してプログラムを走らせます。途中、ポップアップがいくつか出てきますが、図10の様に進んで下さい(『Googleドライブに接続』をクリック→自分のアカウントを選択→『次へ』をクリック→下へスクロール→『続行』をクリック)。これらの操作によって、分析に用いる架空のデータが生成されます。

図10.ポップアップへの対応

以下が、架空のデータを生成するプログラムです。

Googleドライブと連携します。

================================================================================
# Google ColabでGoogleドライブをマウントする
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリを読み込みます。ライブラリとは、特定の機能や処理を簡単に使えるようにまとめたプログラムの集まりです。ライブラリをインポートするだけで、複雑な処理を効率的に行えます。ここでは、データ解析用ライブラリであるpandasとnumpyをインポートします。

================================================================================
#必要なライブラリをインポート
import pandas as pd
import numpy as np
================================================================================

ここで、作り出す架空のデータのサンプル数を決めます。

================================================================================
# ダミーデータの行数（サンプル数）
サンプル数 = 100
================================================================================

何度実行しても、同じ結果が得られるように設定します。

================================================================================
# ランダムシードを設定（再現性のため）
np.random.seed(42)
================================================================================

説明変数(広告費、価格、気温)を生成します。

================================================================================
# 説明変数の生成
広告費 = np.random.uniform(1000, 10000, サンプル数) # 広告費
価格 = np.random.uniform(50, 150, サンプル数) # 価格
気温 = np.random.uniform(15, 35, サンプル数) # 気温
================================================================================


目的変数(売上)を生成します。そして、仮の回帰分析の方程式を設定します。

================================================================================
# 売上（目的変数）の生成
# 仮の回帰式: 売上 = 広告費の影響 + 価格の影響 + 気温の影響 + 誤差
売上 = (
0.05 * 広告費 # 広告費の影響
- 20 * 価格 # 価格の影響
+ 10 * 気温 # 気温の影響
+ np.random.normal(0, 500, サンプル数) # 誤差
)
================================================================================

データを格納します。

================================================================================
# データフレームにまとめる
データ = pd.DataFrame({
"広告費": 広告費,
"価格": 価格,
"気温": 気温,
"売上": 売上
})
================================================================================

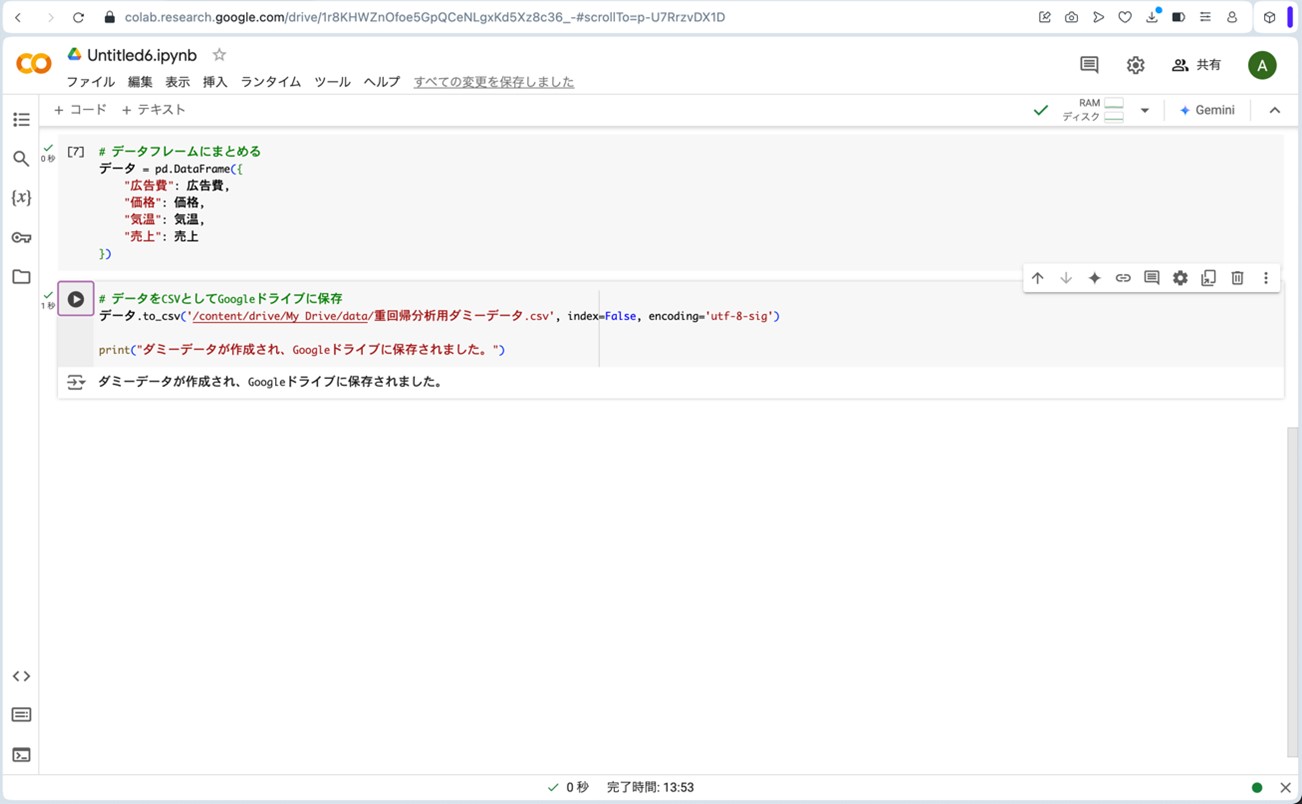
データをcsvファイルとしてGoogleドライブに保存します。保存が完了すると「ダミーデータが作成され、Googleドライブに保存されました。」というメッセージが表示されます。

================================================================================
# データをCSVとしてGoogleドライブに保存
データ.to_csv('/content/drive/My Drive/data/重回帰分析用ダミーデータ.csv', index=False, encoding='utf-8-sig')

print("ダミーデータが作成され、Googleドライブに保存されました。")
================================================================================

図11.Google Colaboratoryにプログラムを読み込ませて、架空のデータを生成

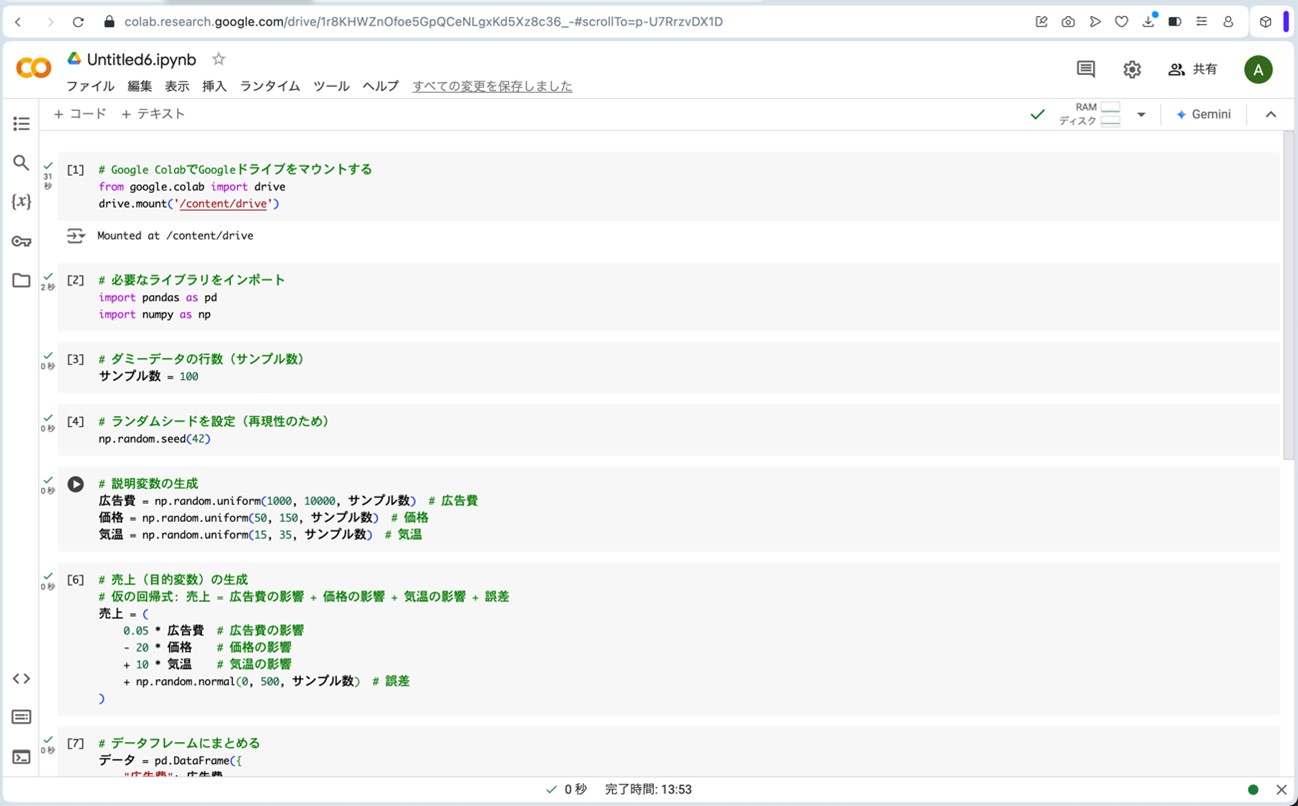
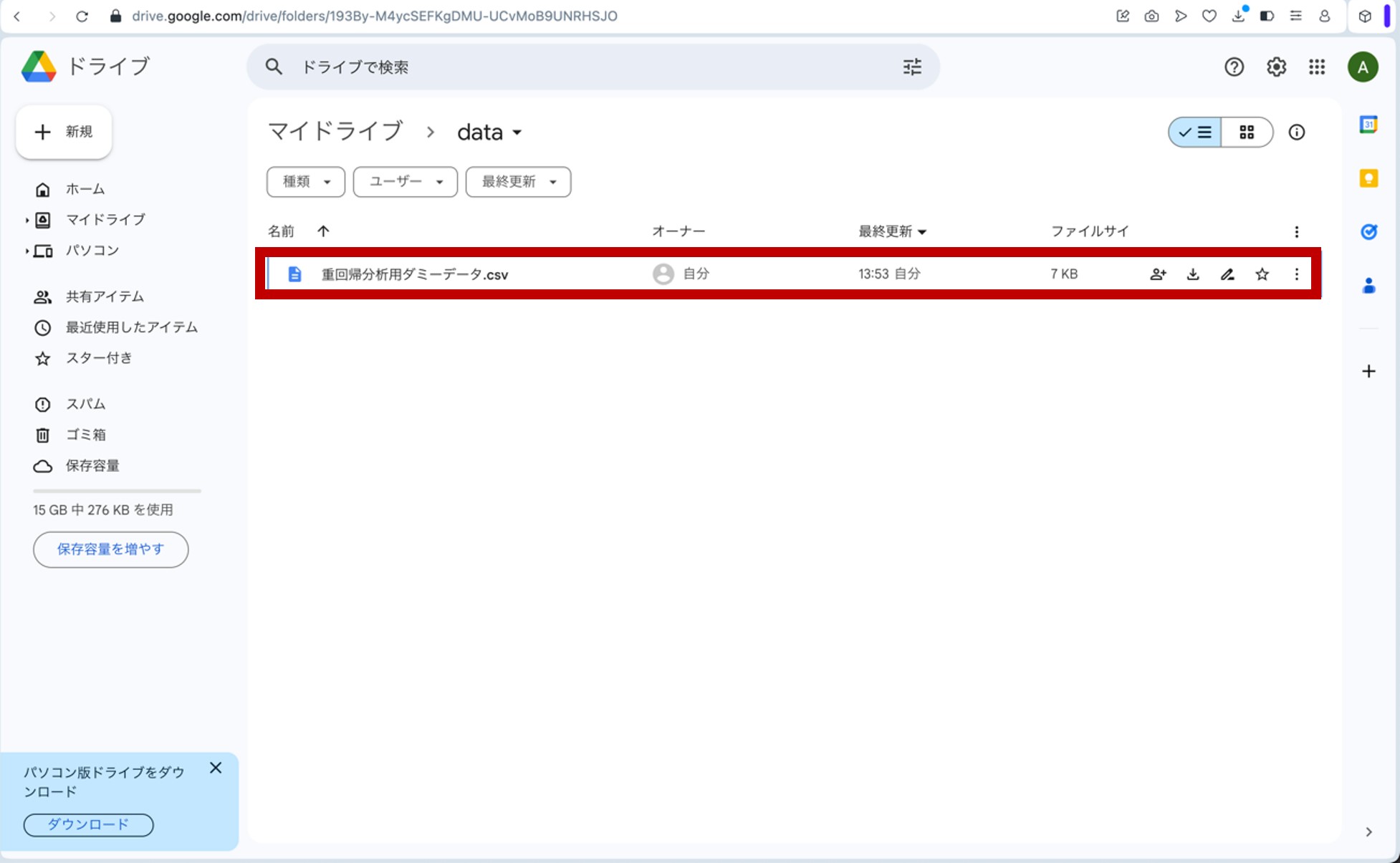
先ほどGoogleドライブのマイドライブ内に作成したdataフォルダをクリックしてみると、重回帰分析用ダミーデータ.csvファイルが格納されているのが確認できます(図12)。

図12.マイドライブの「data」フォルダへ「重回帰分析用ダミーデータ.csv」が格納されている

次に、Google Colaboratoryに戻ります。図3〜7の手順を参考に、図8の画面まで進みます。ここで、以下のプログラムをコピーして、コードセルに貼り付けます。そして、▷ボタンを押して、プログラムを走らせると、重回帰分析の結果と標準化偏回帰係数を用いた重回帰分析の結果が算出されます。

重回帰分析のデモ分析

まずは重回帰分析のプログラムです。ある商品の売上を目的変数とし、広告費・価格・気温を説明変数とした重回帰分析の方程式を考えます。

Googleドライブと連携します。

================================================================================
# Googleドライブをマウント
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
# 必要なライブラリのインポート
import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
================================================================================

データを読み込みます。

================================================================================
# データの読み込み
ファイルパス = '/content/drive/My Drive/data/重回帰分析用ダミーデータ.csv'
データ = pd.read_csv(ファイルパス, encoding='utf-8-sig')
================================================================================

データが正しく読み込まれているか確認します。

================================================================================
# データの確認
print(データ.head())
================================================================================

説明変数と目的変数を設定します。

================================================================================
# 説明変数（広告費、価格、気温）と目的変数（売上）を設定
X = データ[['広告費', '価格', '気温']] # 説明変数
y = データ['売上'] # 目的変数
================================================================================

重回帰分析の方程式がデータの全体的な傾向を適切に表せるように、定数項を追加します。

================================================================================
# 定数項を追加（切片を含める）
X = sm.add_constant(X)
================================================================================

重回帰分析を実行する。

================================================================================
# 重回帰分析の実行
モデル = sm.OLS(y, X).fit()
================================================================================

結果を表示します。

================================================================================
# 回帰結果の概要を表示
print(モデル.summary())
================================================================================

VIFを計算します。

================================================================================
# VIF（分散拡大係数）の計算
vif_data = pd.DataFrame()
vif_data["変数"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
================================================================================

VIFの計算結果を表示します。

================================================================================
# VIFの結果を表示
print("\nVIF（分散拡大係数）:")
print(vif_data)
================================================================================

図13.サンプルプログラムで重回帰分析の結果を算出

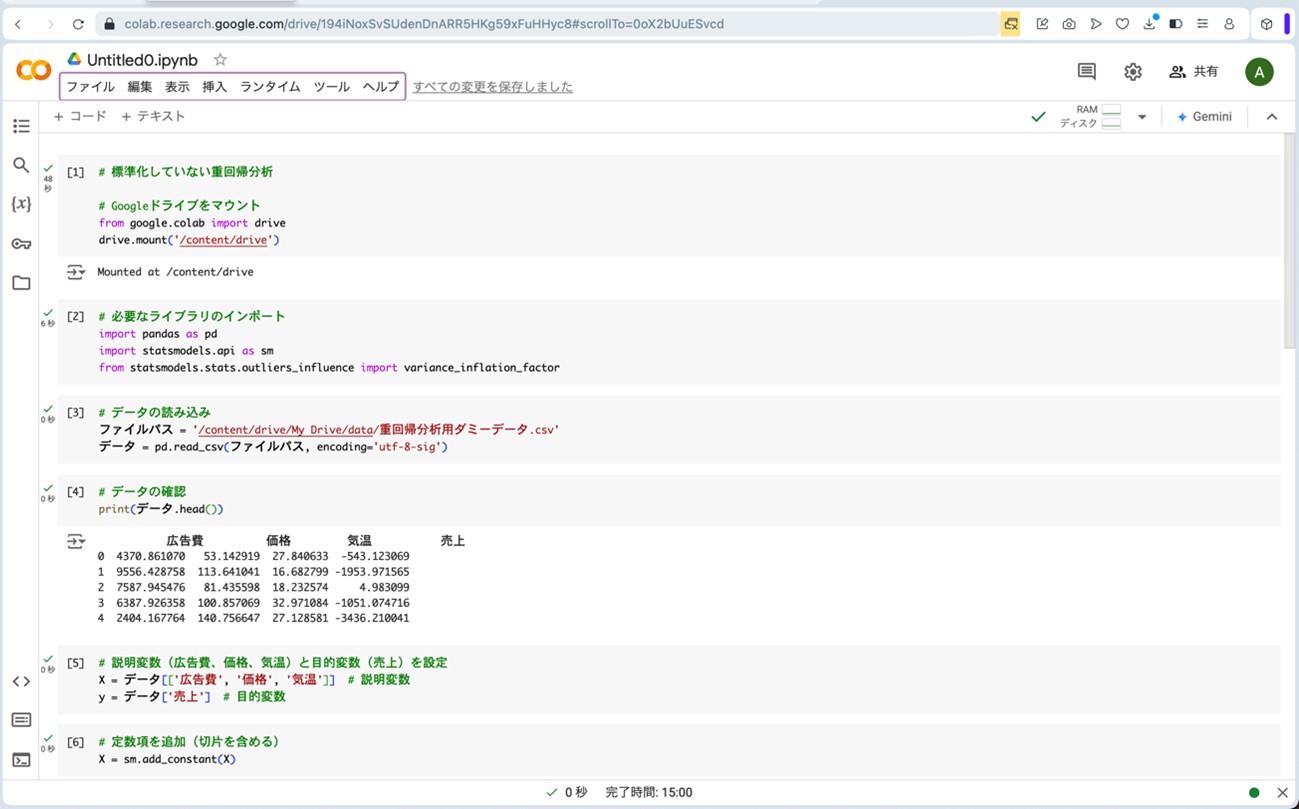
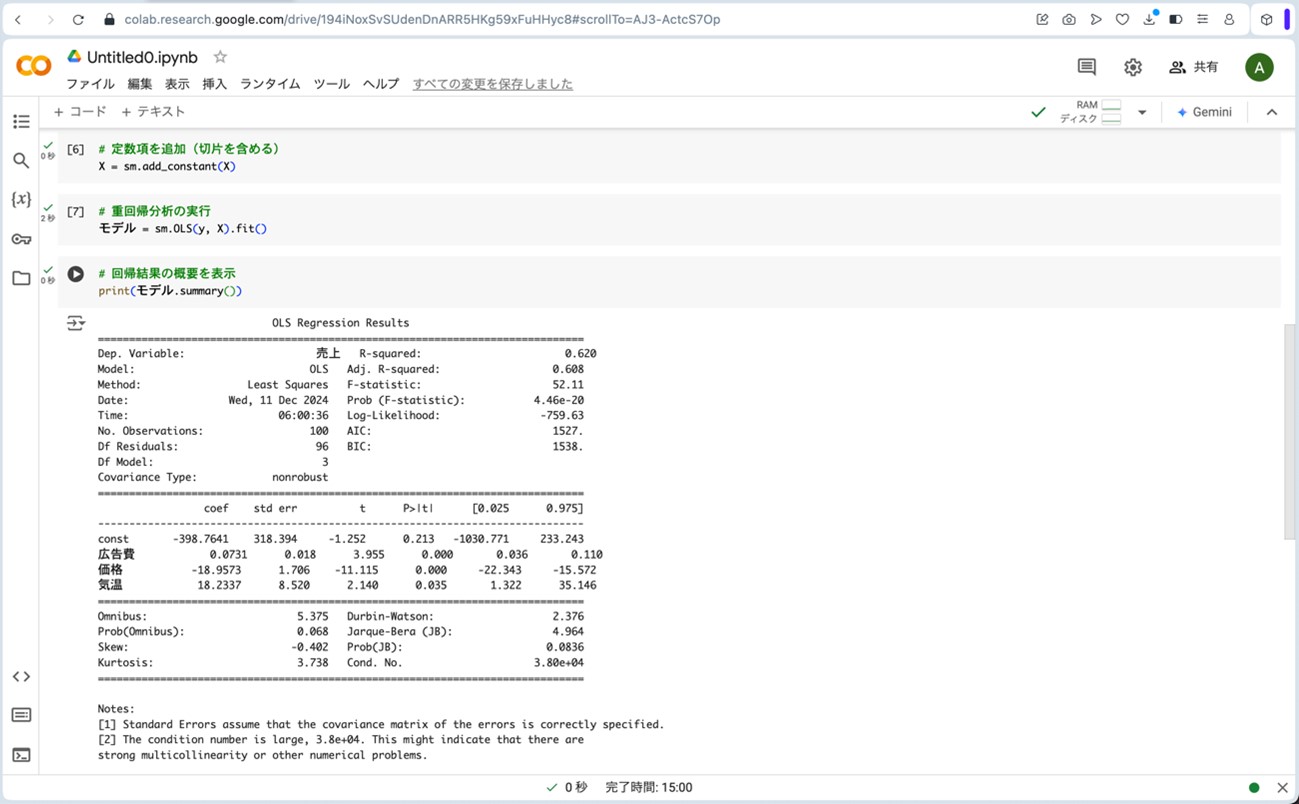
図14.拡大した重回帰分析の結果

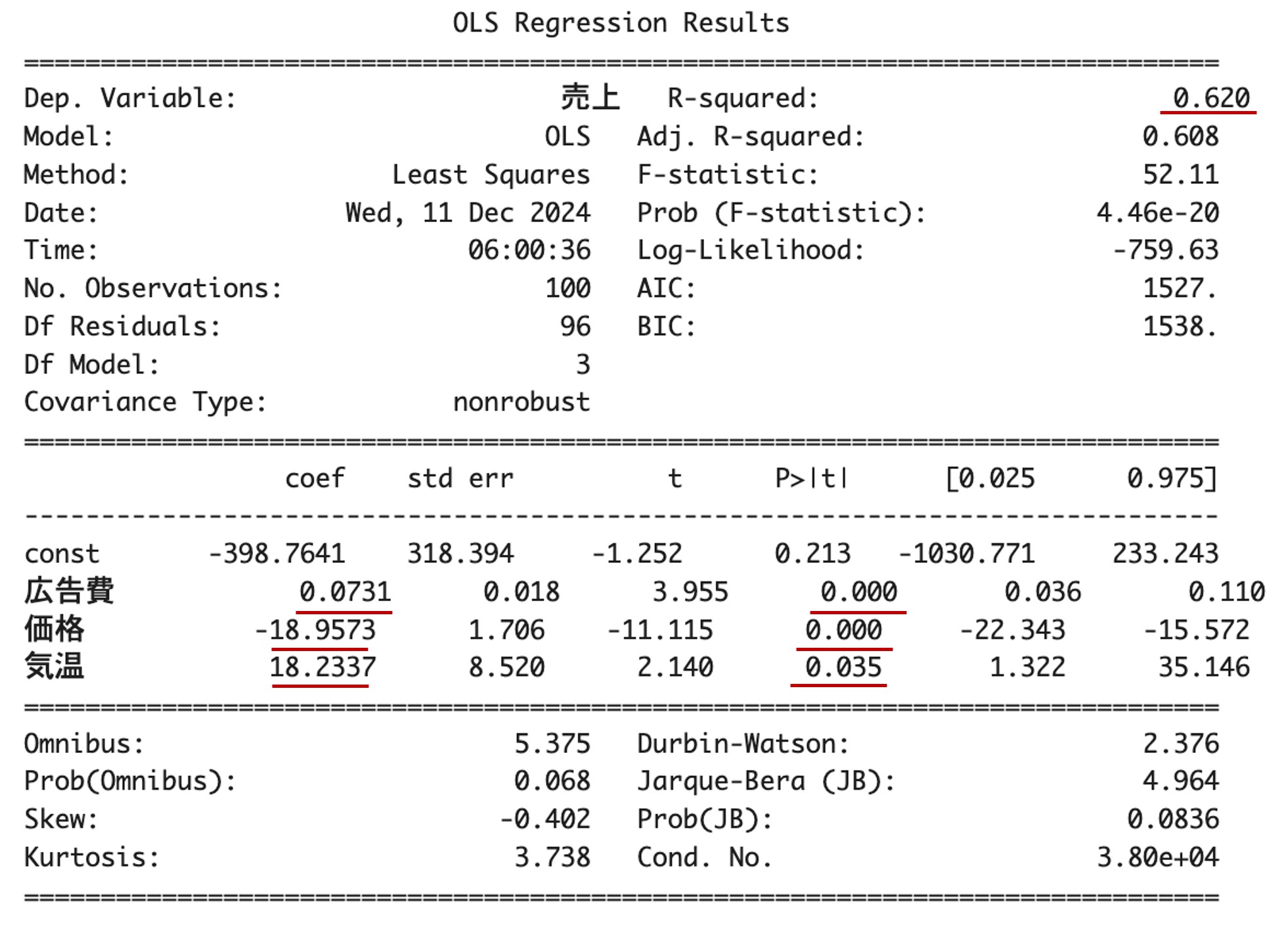
結果を解釈していきましょう。

1. 決定係数 (R2)が0.620ということは、この重回帰分析の方程式は、売上(目的変数)の変動を説明変数(広告費、価格、気温)によって62%を説明できているということを示しています。このことから、この重回帰分析はそれなりの説明力を持つと言えます。
2. 説明変数(広告費、価格、気温)のp値は全て0.05以下なので、説明変数の回帰係数は全て統計的に意味のある値であると言えます。
3. VIFは全ての説明変数(広告費、価格、気温)において1程度であり、10を大幅に下回っていることから、多重共線性の影響の可能性は非常に低いと言えます。
4. 広告費：回帰係数b1=0.0731なので、広告費が1単位増加すると売上が 0.0731 増加します。広告費の単位が「万円」と仮定すると、以下のように解釈できます。現在の広告費が 100万円 の場合、広告費を 120万円 に増やす（+20万円）とします。この場合、売上の増加 = 0.0731×200000=14620なので、売上は14,620円増加すると予測されます。この結果から、広告費の投資効果は非常に小さいと考えられます。
5. 価格：回帰係数b2=-18.9573なので、価格が1単位増加すると売上が 18.9573 減少します。価格の単位が「円」と仮定すると、以下のように解釈できます。現在の価格が 1,000円 の商品を 1,100円 に値上げする（+100円）とします。売上の減少 = −18.9573×100=−1,895.73なので、売上は1,895.73円減少すると予測されます。この結果から、価格の上昇は売上を大きく減少させるため、慎重に検討する必要があると言えます。
6. 気温：回帰係数b3＝18.2337なので、気温が1単位上昇すると売上が 18.2337 増加します。気温の単位が「℃」であると仮定すると、以下のように解釈できます。現在の気温が 25℃ で、気温が 30℃ に上昇した（+5℃）とします。売上の増加 = 18.2337×5=91.1685なので、売上は91.1685円増加すると考えられます。気温の上昇が売上にプラスの影響を与えるため、気温が高くなる季節にはプロモーションを強化する戦略が多少の効果を持つと考えられます。

標準化偏回帰係数を用いた重回帰分析のデモ分析

次に標準化偏回帰係数を用いた重回帰分析のプログラムです。アイスクリームの売上を目的変数とし、広告費・価格・気温を説明変数とした方程式を考えます。

Googleドライブに接続します。

================================================================================
# Googleドライブをマウント
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
# 必要なライブラリのインポート
import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.preprocessing import StandardScaler

データを読み込みます。

================================================================================
[b]# データの読み込み
ファイルパス = '/content/drive/My Drive/data/重回帰分析用ダミーデータ.csv'
データ = pd.read_csv(ファイルパス, encoding='utf-8-sig')
================================================================================

データが正しく読み込まれているか確認します。

================================================================================
# データの確認
print("データの冒頭5行:")
print(データ.head())
================================================================================

説明変数（広告費、価格、気温）と目的変数（売上）を設定します。

================================================================================
# 説明変数（広告費、価格、気温）と目的変数（売上）を設定
X = データ[['広告費', '価格', '気温']] # 説明変数
y = データ['売上'] # 目的変数
================================================================================

説明変数と目的変数を標準化（平均0、標準偏差1、-1〜1の間の値に変換すること）の準備をします。

================================================================================
# 説明変数と目的変数の標準化
scaler = StandardScaler()
================================================================================

説明変数を標準化します。

================================================================================
# 説明変数の標準化
X_standardized = scaler.fit_transform(X)
X_standardized = pd.DataFrame(X_standardized, columns=['広告費', '価格', '気温'])
================================================================================

重回帰分析の方程式がデータの全体的な傾向を適切に表せるように、定数項を追加します。

================================================================================
# 定数項を追加（切片を含める）
X_standardized = sm.add_constant(X_standardized)
================================================================================

目的変数を標準化します。

================================================================================
# 目的変数の標準化
y_standardized = scaler.fit_transform(y.values.reshape(-1, 1)).flatten()
================================================================================

標準化偏回帰係数を用いた重回帰分析を実行します。

================================================================================
# 標準化後の重回帰分析
モデル_標準化 = sm.OLS(y_standardized, X_standardized).fit()
================================================================================

分析結果を表示します。

================================================================================
# 標準化後の回帰結果を表示
print("\n目的変数も標準化した回帰結果（標準化偏回帰係数）:")
print(モデル_標準化.summary())
================================================================================

VIFを計算します。

================================================================================
# VIF（分散拡大係数）の計算
X_with_const = sm.add_constant(X) # 定数項を含めたデータ
vif_data = pd.DataFrame()
vif_data["変数"] = X_with_const.columns
vif_data["VIF"] = [variance_inflation_factor(X_with_const.values, i) for i in range(X_with_const.shape[1])]
================================================================================

VIFの計算結果を表示します。

================================================================================
# VIFの結果を表示
print("\nVIF（分散拡大係数）:")
print(vif_data)
================================================================================

図15.サンプルプログラムで標準化偏回帰係数を用いた重回帰分析の結果を算出

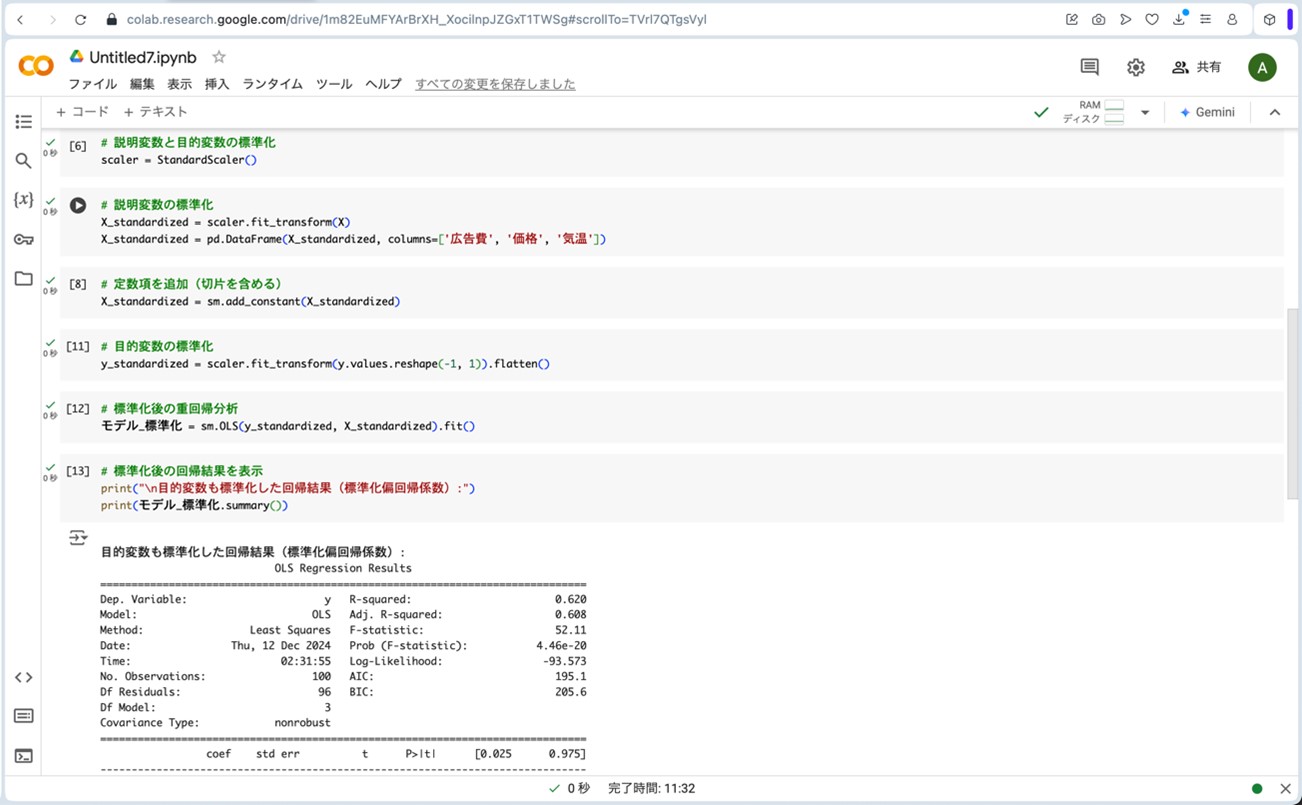
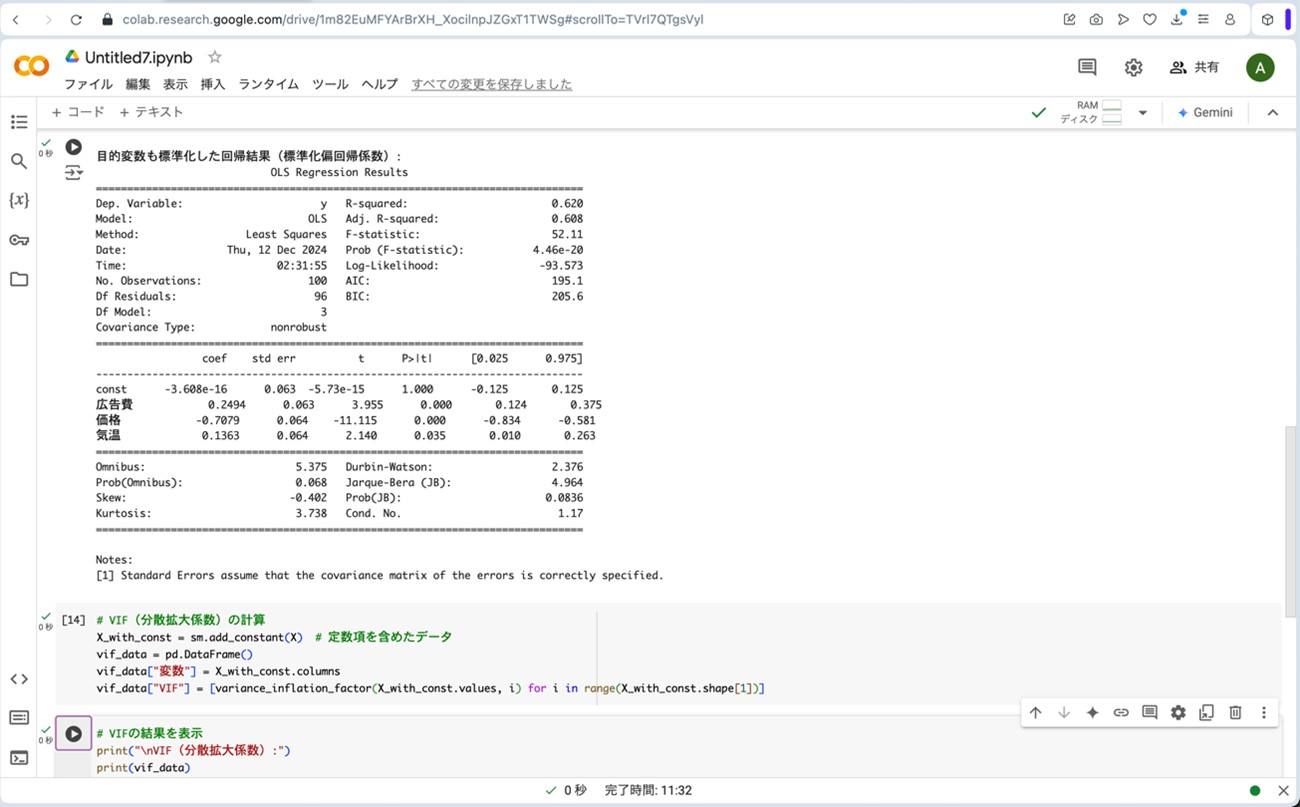
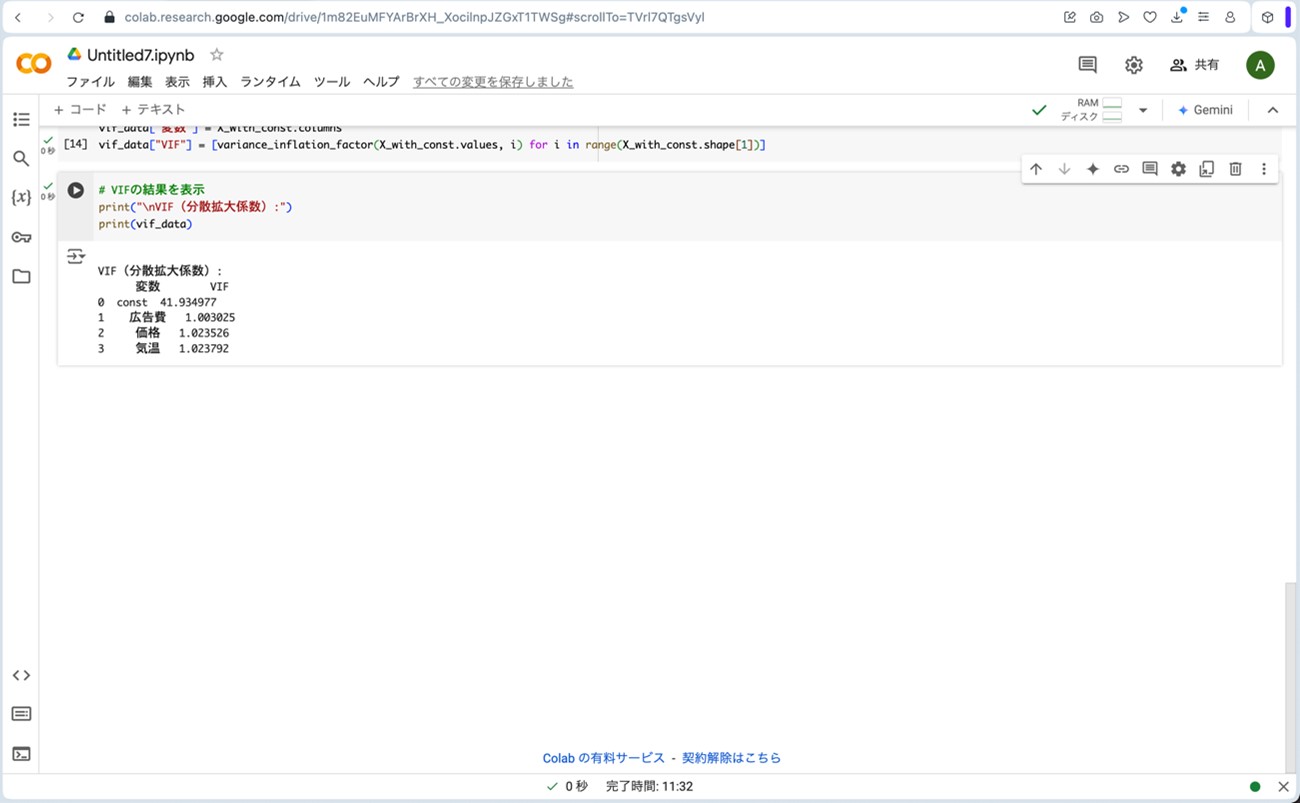
図16.拡大した標準化偏回帰係数を用いた重回帰分析の結果

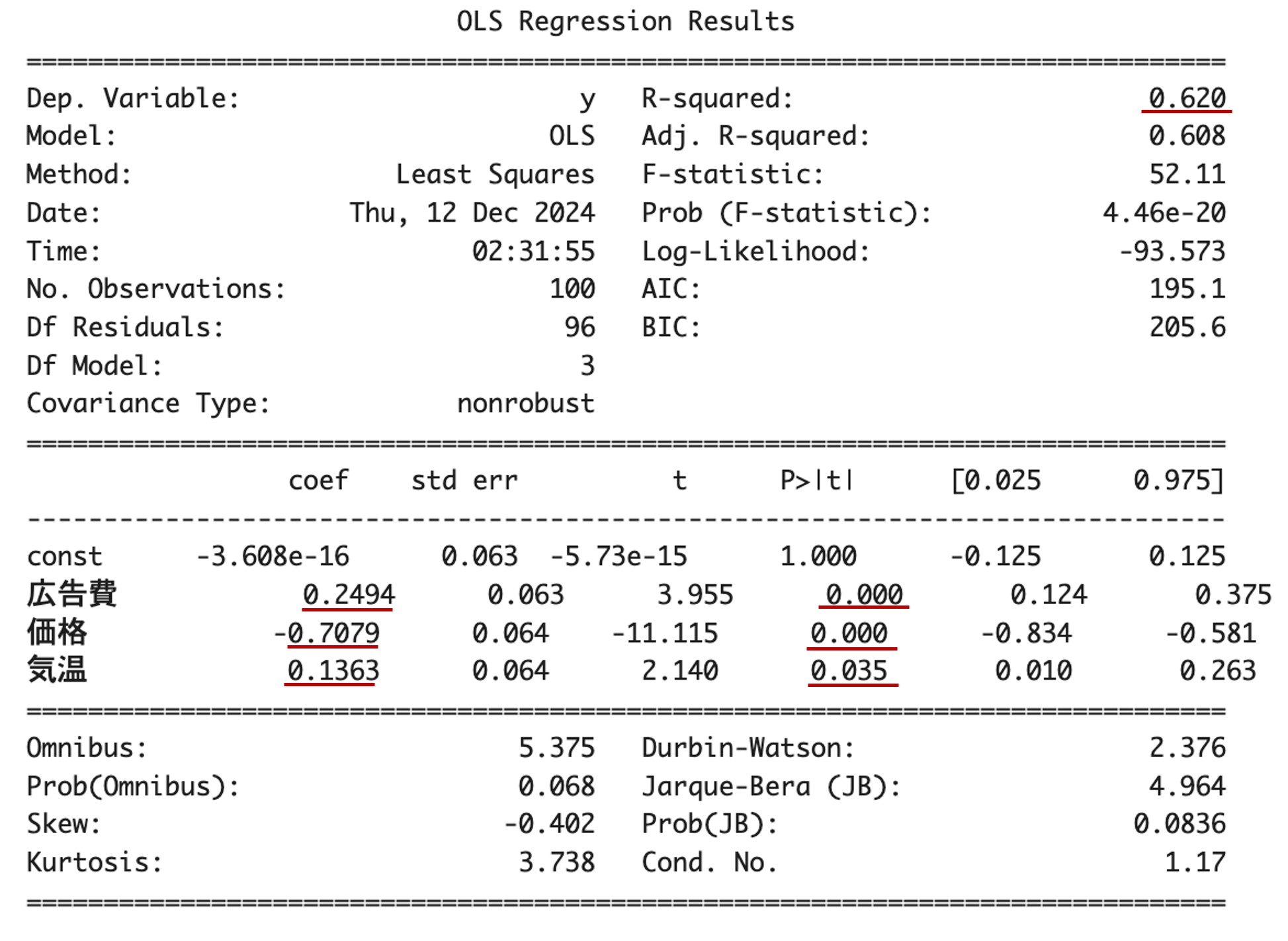
結果を解釈していきましょう。

1. 決定係数 (R2)が0.620で、先ほどの標準化偏回帰係数を用いない重回帰分析の方程式と同じ結果です。売上(目的変数)の変動を説明変数(広告費、価格、気温)によって62%を説明できているということを示しています。このことから、この重回帰分析はそれなりの説明力を持つと言えます。
2. 説明変数(広告費、価格、気温)のp値は全て0.05以下で、先ほどの標準化偏回帰係数を用いない重回帰分析の方程式と同じ結果なので、説明変数の回帰係数は全て統計的に意味のある値であると言えます。
3. VIFは先ほどの標準化偏回帰係数を用いない重回帰分析の方程式と同じ結果で、全ての説明変数(広告費、価格、気温)において1程度であり、10を大幅に下回っていることから、多重共線性の影響の可能性は非常に低いと言えます。
4. 広告費：広告費(β=0.2494)は、売上に正の影響を与えていますが、価格ほどの影響力はありません。この結果から、広告効果を高めるためには、より効率的な広告運用が必要です。
5. 価格：価格(β=−0.7079)は、最も大きな影響を持つ変数であり、売上に強い負の影響を与えます。この結果から、価格は売上に最も強い負の影響を与えるため、価格戦略が売上に大きく影響します。価格設定には特に注意が必要です。
6. 気温：(β=0.1363) は、売上に最も小さい正の影響を持っています。この結果から、気温が高くなる季節に合わせてマーケティング施策を調整することが、多少の効果を持つと考えられます。

Googleドライブを利用される際はこちらをご確認、ご理解の上ご利用ください。

Google ドライブ利用規約

ドライブにおけるユーザーのプライバシー保護とユーザー自身による管理
Google ドライブ ヘルプ

※Googleドライブの説明に使用している各図は、GoogIeのウェブページを撮影して掲載しています。

1. 所属等は執筆当時のもので、現在とは異なる場合があります。
2. また記事中の技術、手法等については、今後の技術の進展、外部環境の変化等によっては、実情と合致しない場合があります。
3. 各記事における最新の動向につきましては、当社までぜひお問い合わせください。

著者プロフィール

プロフェッショナルズストラテジックプランニング局データソリューション部渡邉 成（わたなべ あきら）

この人の書いた記事

• 連載！データ分析②：回帰分析
• 連載！データ分析①：相関係数

得意領域

• #データアナリシス
• #機械学習
• #デジタル

著者について詳しく見る