データサイエンス 統計学 データ分析 機械学習 AI マーケティング 2025.03.14
連載！データ分析③：ロジスティック回帰分析

ロジスティック回帰分析とは？

データ分析や統計モデリングの世界では、「結果を予測するための方法」としてさまざまな手法が用いられています。その中でも、ロジスティック回帰分析は、特に「結果が2つのカテゴリーに分かれる場合」に活躍する手法として知られています。例えば、「購入するか、しないか」「合格するか、不合格か」「病気にかかるか、かからないか」というような問題に適した分析手法です。
「回帰分析」と聞くと、従来の回帰分析を思い浮かべる方も多いかもしれません。従来の回帰分析では、数値データを基にして、ある変数（目的変数：予測したい値）を他の変数（説明変数：目的変数に影響を与える要因の値）から予測します。しかし、ロジスティック回帰分析では、結果が「カテゴリー」であるため、単純な数値の予測ではなく、ある事象が発生する/発生しない確率を予測することに重点を置きます。
例えば、「広告を見た人が商品を購入する確率」を予測する場合、ロジスティック回帰分析を使えば、「この条件のときに購入する確率は70%だ」という形で結果を解釈することが可能です。この確率の予測は、マーケティング、医療、教育など、多岐にわたる分野で意思決定をサポートする強力なツールとなります。
この手法を深く理解するためには、ロジスティック回帰分析が「どのようにデータを扱い」「どのように確率を導き出すのか」という仕組みを知ることが重要です。次章では、この手法の具体的な仕組みや応用例について、さらに掘り下げて解説していきます。

ロジスティック回帰分析の仕組みを理解しよう

ロジスティック回帰分析がどのようにして結果を予測するのか、数式は割愛しながら、その仕組みを分かりやすく解説します。この手法の基盤となるのは、「ロジット関数」と呼ばれる関数を使った変換です。この関数を使うことで、ある事象が発生する/発生しないという問題に対して「0から1の範囲で確率を表現する」ことが可能になります。

ロジット関数とシグモイド関数

ロジスティック回帰では、結果（目的変数）が「0」または「1」に分類されると仮定します。「1」は「事象が起きる」、つまりポジティブな結果を示し、「0」は「事象が起きない」、つまりネガティブな結果を示します。
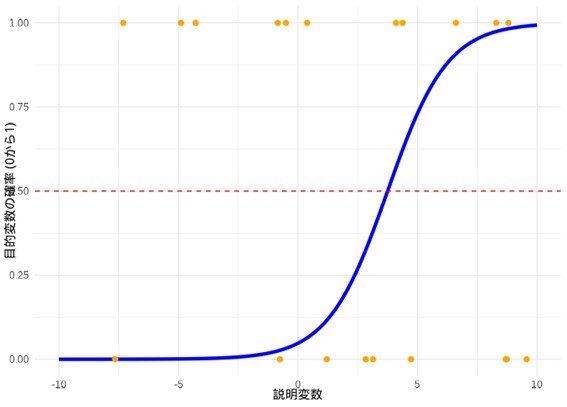
ロジット関数は、目的変数を「0」または「1」の二択から、確率（0～1）に変換するための仕組みです。これにより、結果がどちらのカテゴリーに属するかを確率的に表現できます。これを実現する曲線の関数が、ロジット関数の逆関数(例えば、掛け算に対する割り算のような操作として逆の関係にある関数)であり、S字型をした「シグモイド関数」です。この関数が、入力されたデータを「0から1の間の確率」に変換する役割を果たします。

図1.シグモイド関数の例

回帰係数の意味と解釈

ロジスティック回帰では、まず従来の回帰分析モデルを作成します。具体的には、説明変数に重み（回帰係数）を掛け算し、それらを足し合わせて予測値を計算します。ただし、このままでは予測値が「0～1の確率」という範囲を超えてしまうことがあります。
ここで、先ほど説明したシグモイド関数が活躍します。この従来の回帰分析の予測値をシグモイド関数に通すことで、結果を0～1の確率に変換するのです。この変換により、「この条件のもとでは事象が起こる確率は85%(0.85)だ」というように、解釈可能な結果が得られます。

モデルの構築と学習

ロジスティック回帰分析では、まず大量のデータをもとに方程式を構築します。この過程では、「説明変数がどれだけ目的変数に影響を与えるか」を示す回帰係数を推定します。このプロセスには、最尤推定法と呼ばれる手法が一般的に用いられます。

出力結果の解釈

モデルが完成した後は、出力された結果を解釈します。ロジスティック回帰では、回帰係数の符号や大きさを見ることで、各説明変数が目的変数に与える影響を評価できます。たとえば、正の回帰係数を持つ説明変数は目的変数に対してポジティブな影響を与え、負の係数を持つ説明変数はネガティブな影響を与えます。また、係数の大きさが大きいほど、その変数の影響が強いことを意味します。

ロジスティック回帰分析の具体例と応用

例えば、あるECサイトが「ユーザーが商品を購入するかどうか」を予測したい場合を考えてみましょう。このとき、ユーザーの行動データを使ってモデルを構築します。ロジスティック回帰分析を用いることで、「このユーザーが商品を購入する確率は75%だ」といった結果を得ることができます。
この予測をもとに、購入確率が高いユーザーには特別なクーポンを配布するなど、ターゲティングを最適化することで売上向上につなげることが可能です。

マーケティングでの活用例：購入予測を数値で解釈する

ロジスティック回帰分析が、前述のようなマーケティング場面においてどのように活用されるのか、具体的な数値例を用いて解説します。ここでは、ECサイトでユーザーの購入予測を行うケースを想定します。
あるECサイトが、以下のデータを使ってユーザーが商品を購入する確率を予測したいとします。目的変数は「ユーザーが商品を購入するかどうか(購入する=1、購入しない=0)」で、説明変数は以下です。

1. 商品ページの閲覧回数（A）
2. カートに入れた回数（B）
3. 過去の購入履歴（C）
   （購入経験あり= 1、なし= 0）

このデータをもとにロジスティック回帰分析を行い、以下のような結果（回帰係数）が得られたと仮定します：

1. 定数項(すべての説明変数が0のときに目的変数が取る値)：-1.5
2. 商品ページの閲覧回数（A）：0.02
3. カートに入れた回数（B）：0.3
4. 過去の購入履歴（C）：1.2

これらの数値を基に、以下の条件を持つユーザーについて、購入する確率を計算してみます。

1. 商品ページの閲覧回数：50回
2. カートに入れた回数：2回
3. 過去の購入履歴：あり（=1）

ロジスティック回帰では、まず「説明変数の影響を合算」してスコアを計算します。このスコアは次のように求められます。

1. 定数項（-1.5）
2. 商品ページの閲覧回数（50回 × 0.02 = 1.0）
3. カートに入れた回数（2回 × 0.3 = 0.6）
4. 過去の購入履歴（1 × 1.2 = 1.2）

これらを合計すると、スコアは1.3になります。
次に、このスコアを基に「確率」を計算します。この確率はロジスティック回帰の特徴であるシグモイド関数によって、スコアを0～1の範囲の値に変換して得られます。計算式はここでは割愛しますが、このスコア（1.3）に基づく確率はおよそ78%となります。
この78%という確率は、「このユーザーが商品を購入する可能性が78%ある」という意味になります。過去に購入経験があることや、カートに商品を入れたという行動が、この結果に大きく影響を与えていると考えられます。一方で、商品ページの閲覧回数も一定の影響を与えていますが、単独ではそれほど強い要因ではないことが分かります。

オッズ比を使った要因の比較

ロジスティック回帰分析で使う指標としてオッズ比というものがあります。オッズ比は各説明変数が目的変数にどの程度影響を与えるかを示す値です。

1. 定数項：-1.5
2. 商品ページの閲覧回数（A）：0.02
3. カートに入れた回数（B）：0.3
4. 過去の購入履歴（C）：1.2

計算式はここでは省略しますが、上記のロジスティック回帰分析の結果から各説明変数のオッズ比を計算すると以下のようになります。

1. 商品ページの閲覧回数（A）：オッズ比=1.02
   →閲覧回数が1回増えるごとに、購入可能性が約2%増加します。
2. カートに入れた回数（B）：オッズ比=1.35
   →カートに入れた回数が1回増えるごとに、購入可能性が約35%増加します。
3. 過去の購入履歴（C）：オッズ比=3.32
   →過去に購入経験があるユーザーは、ないユーザーに比べて購入可能性が約3.32倍になります。

分析環境の構築

さて、本連載の最後には、Pythonというプログラム言語を使ってデータ分析をする方法が記載されています。それには事前準備(環境構築)が必要です。

プログラムを動かすために使用するのが、Google社の提供する、Google Colaboratory とGoogleドライブです。具体的には、Google Colaboratory 上でプログラムを動かして、Googleドライブに格納したデータを呼び出して分析する、という仕組みになっています。

以下に、その事前準備の方法を解説していきます。

Googleドライブ

まずは、Googleドライブからです。Googleのアカウントを持っている人はサインイン、Googleのアカウントを持っていない人はアカウントを作成(サインアップ)し、上記のリンクからGoogleドライブに飛んで下さい。すると、図3のようなホーム画面が出てきます。

図3.Googleドライブのホーム画面

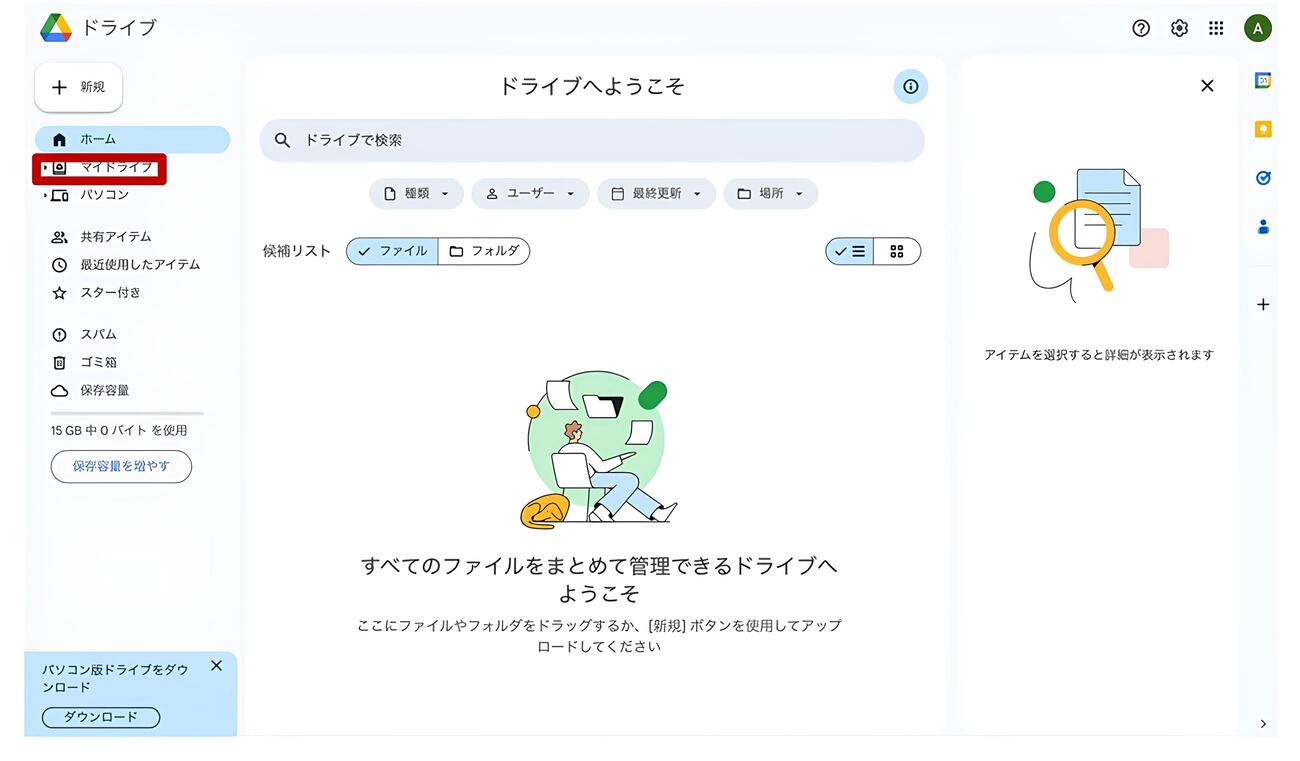
左上の『マイドライブ』をクリックすると、図3のような画面が現れます。自分で入れたファイルはまだありませんが、ここに、これからの連載ごとに使用するデータを格納していきます。

図3.マイドライブの中身

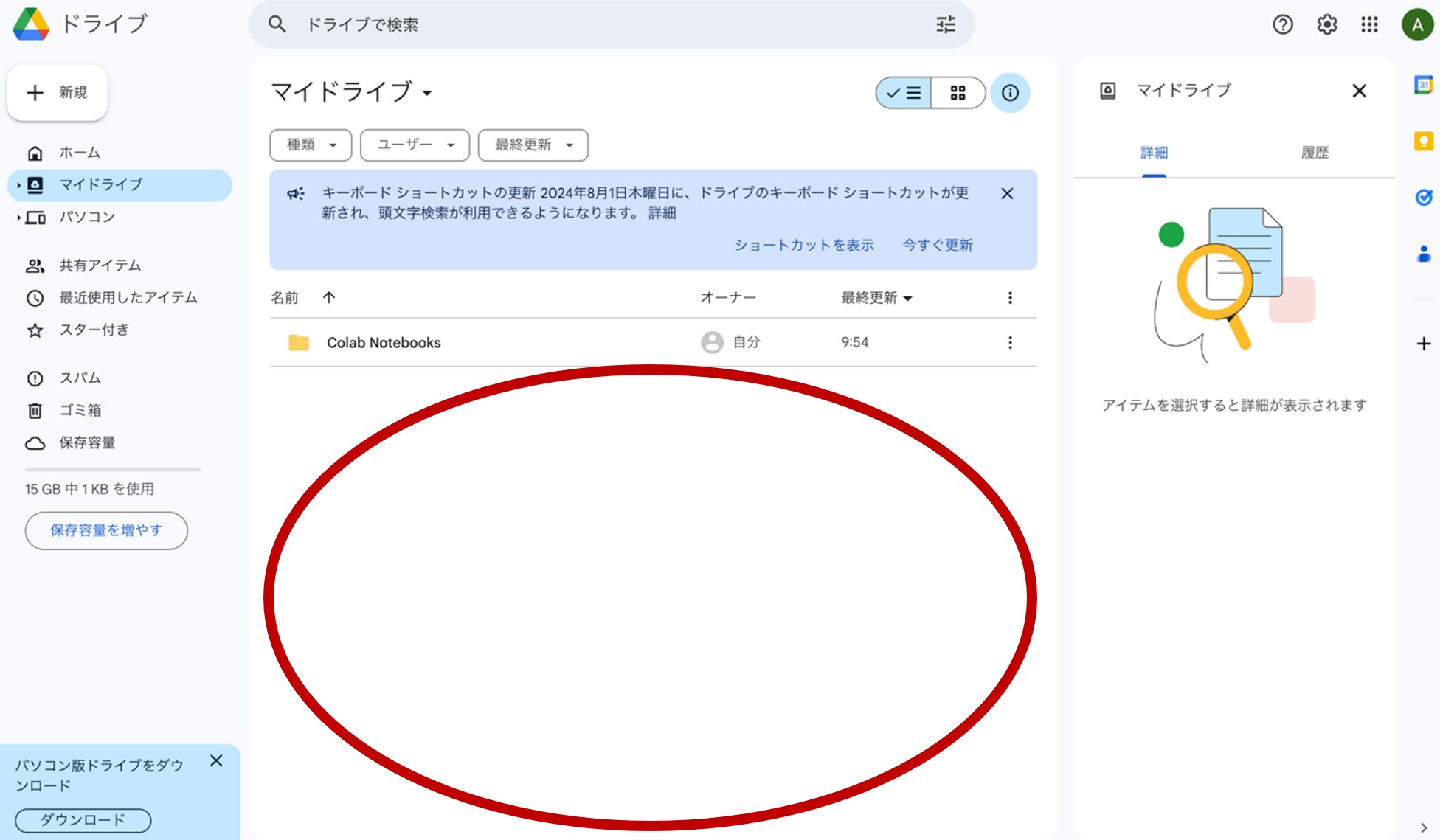
画面中央下の空白(図3の赤丸部分)を右クリックして下さい。すると図4のような表示が現れます。ここから、Google Colaboratoryの設定をしていきます。

図4.Google Colaboratoryを追加

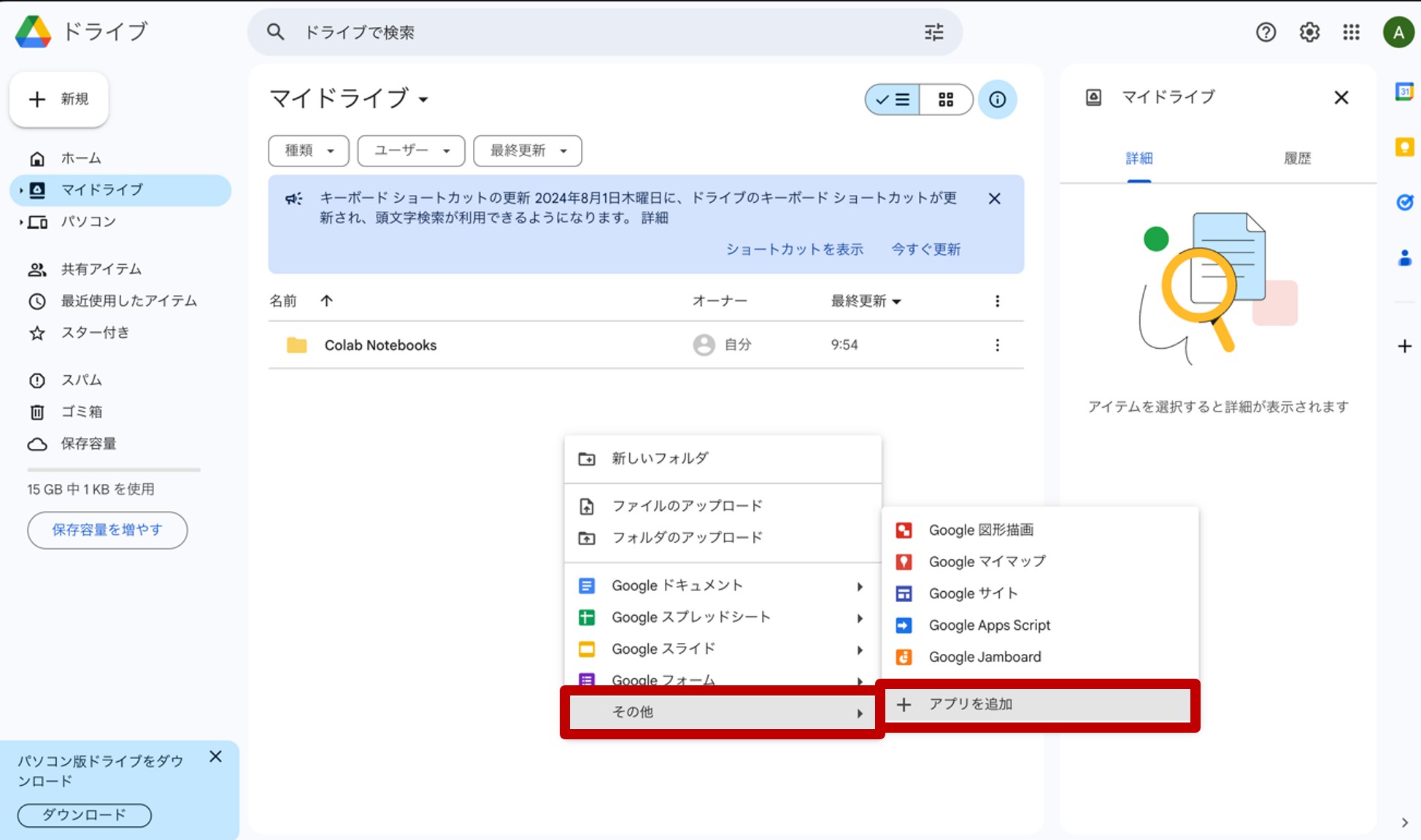
ここで、『その他』→『アプリを追加』をクリックします。

図5.Google Colaboratoryをインストール

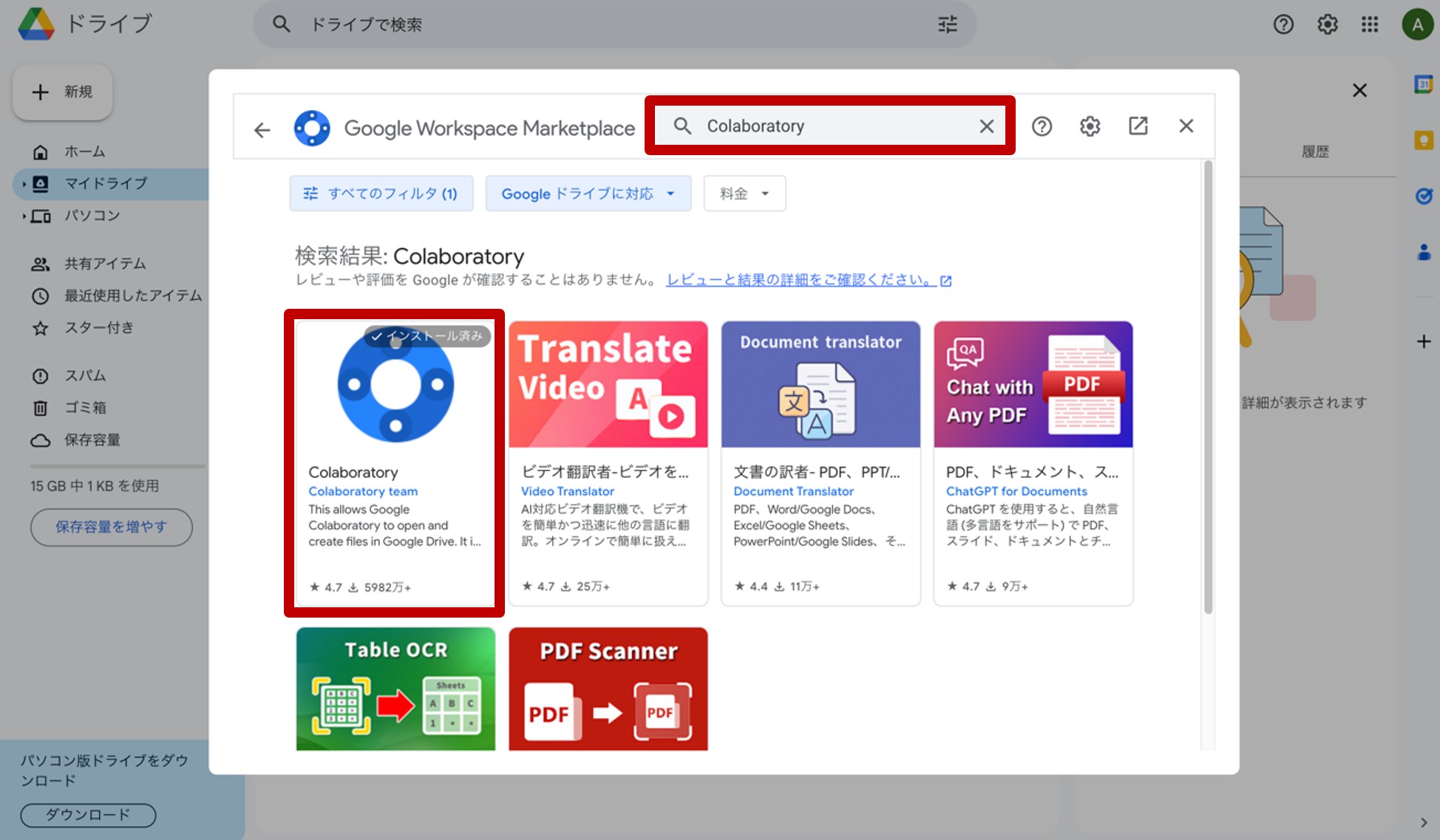
現れた画面の検索窓に『Colaboratory』と入力して検索し、インストールして下さい(図5)。以上で、Googleドライブ上での下準備は終了です。

Google Colaboratory

次に、Google Colaboratoryです。上記のリンクから飛ぶと、図6の様なホーム画面が現れます。

図6.Google Colaboratoryのホーム画面

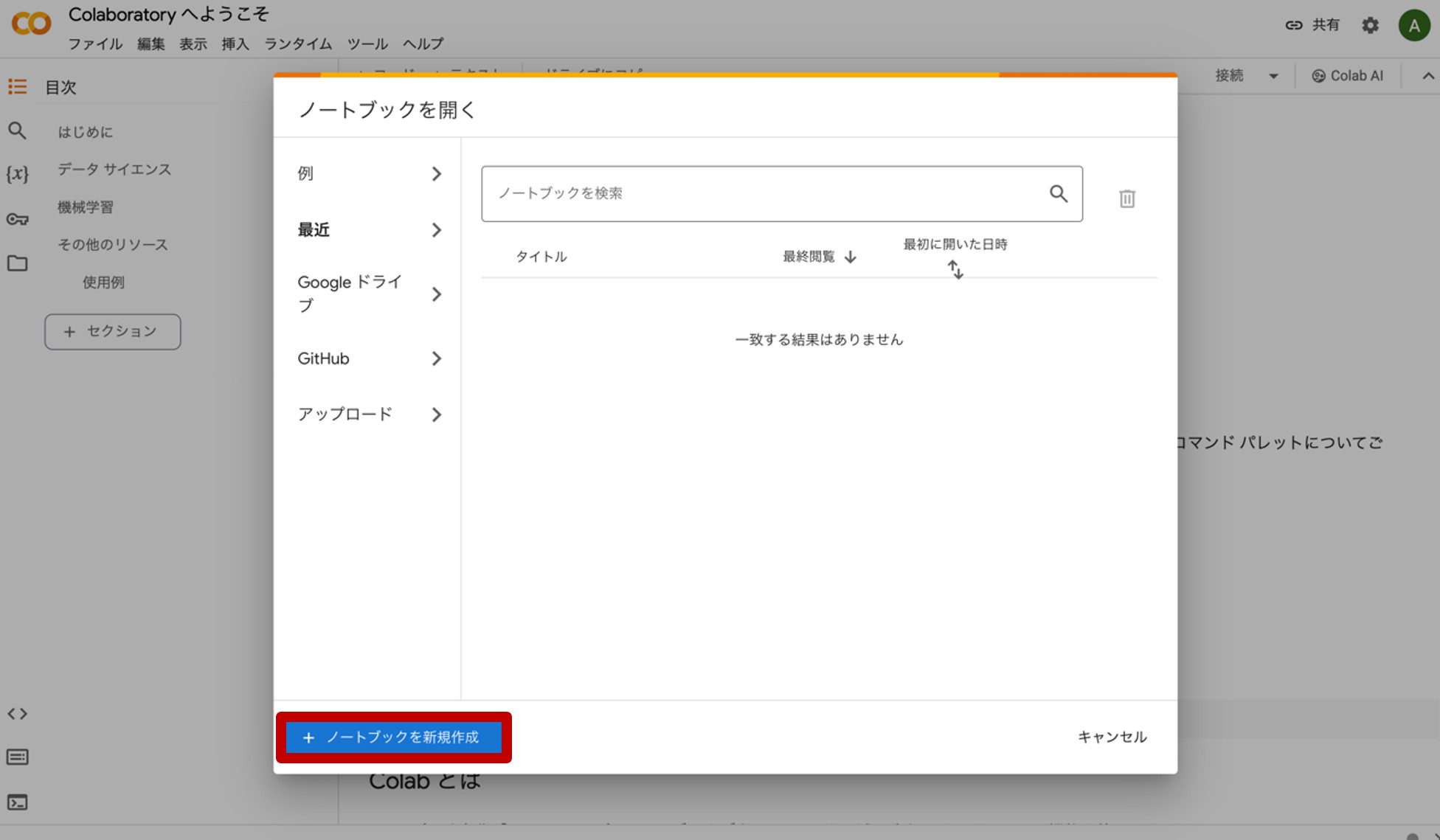
画面下側にある『ノートブックを新規作成』をクリックすると、図7のような画面が現れます。

図7.Google Colaboratoryのプログラムとテキスト入力画面

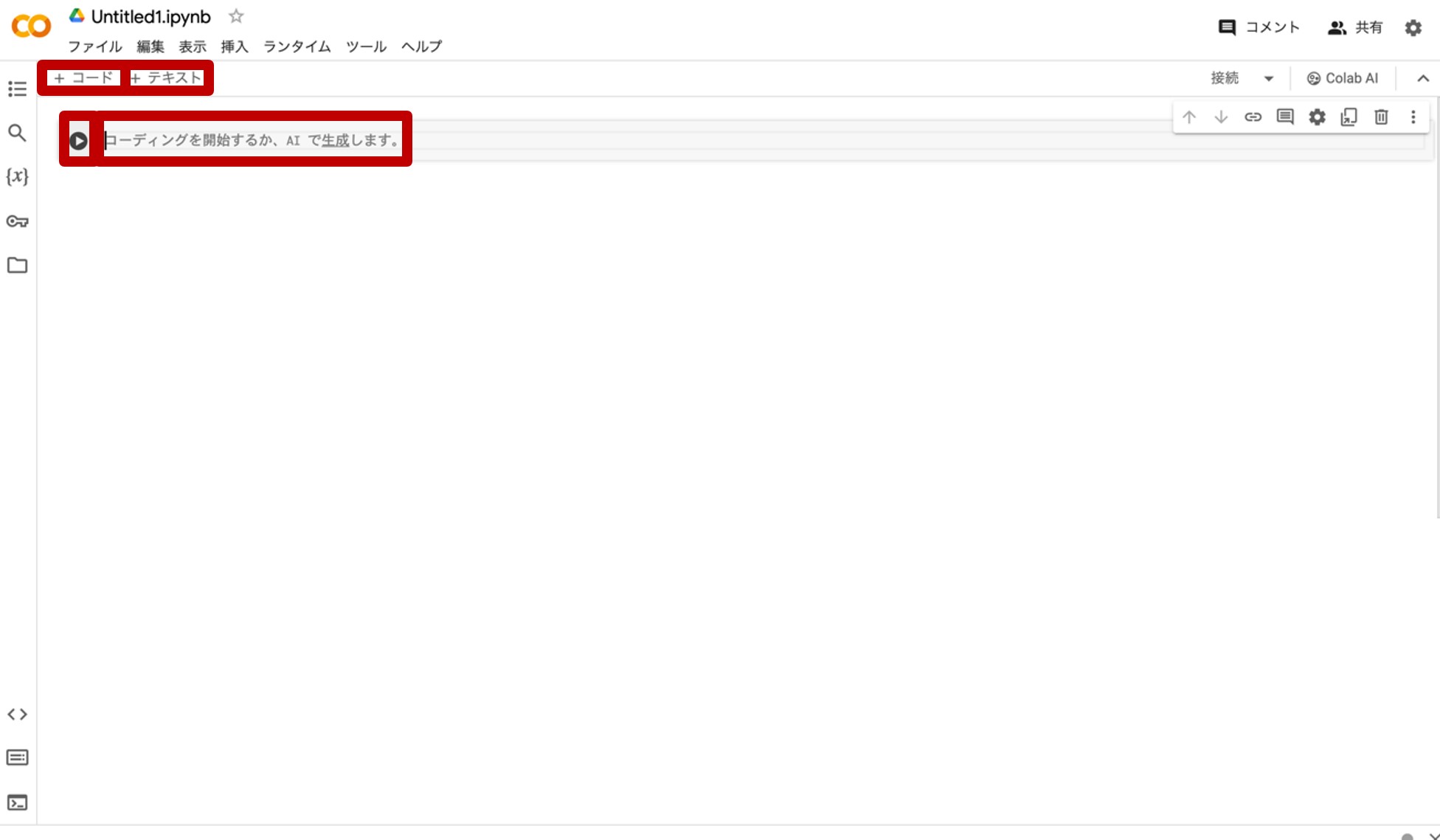
『コーディングを開始するか、AIで生成します。』とあるのが、プログラムを書き込む場所であるコードセルです(AI生成については本連載では省略します。)。左の▷ボタンを押すと当該プログラムが走り出します。分割してプログラムを書きたいときは、その上の『+コード』をクリックするとコードセルを追加することができます。
次に、『+テキスト』をクリックすると出現するのが、コードセルにあるプログラムの解説やメモを書くことができる「テキストセル」です。
以上で下準備は終了です。ここで構築した分析環境を、各連載のデモ分析の際に役立てて下さい。

実際のデータとPythonのプログラム

以下に、Pythonを用いて架空のデータを生成する方法と、ロジスティック回帰分析を実行するPythonのプログラムを用意しています。
実際にみなさんのお手元のPCで計算して、実際の分析がどのような感覚か、まずは直感的に味わってみましょう(プログラムの文法等はひとまず置いておきましょう。)。
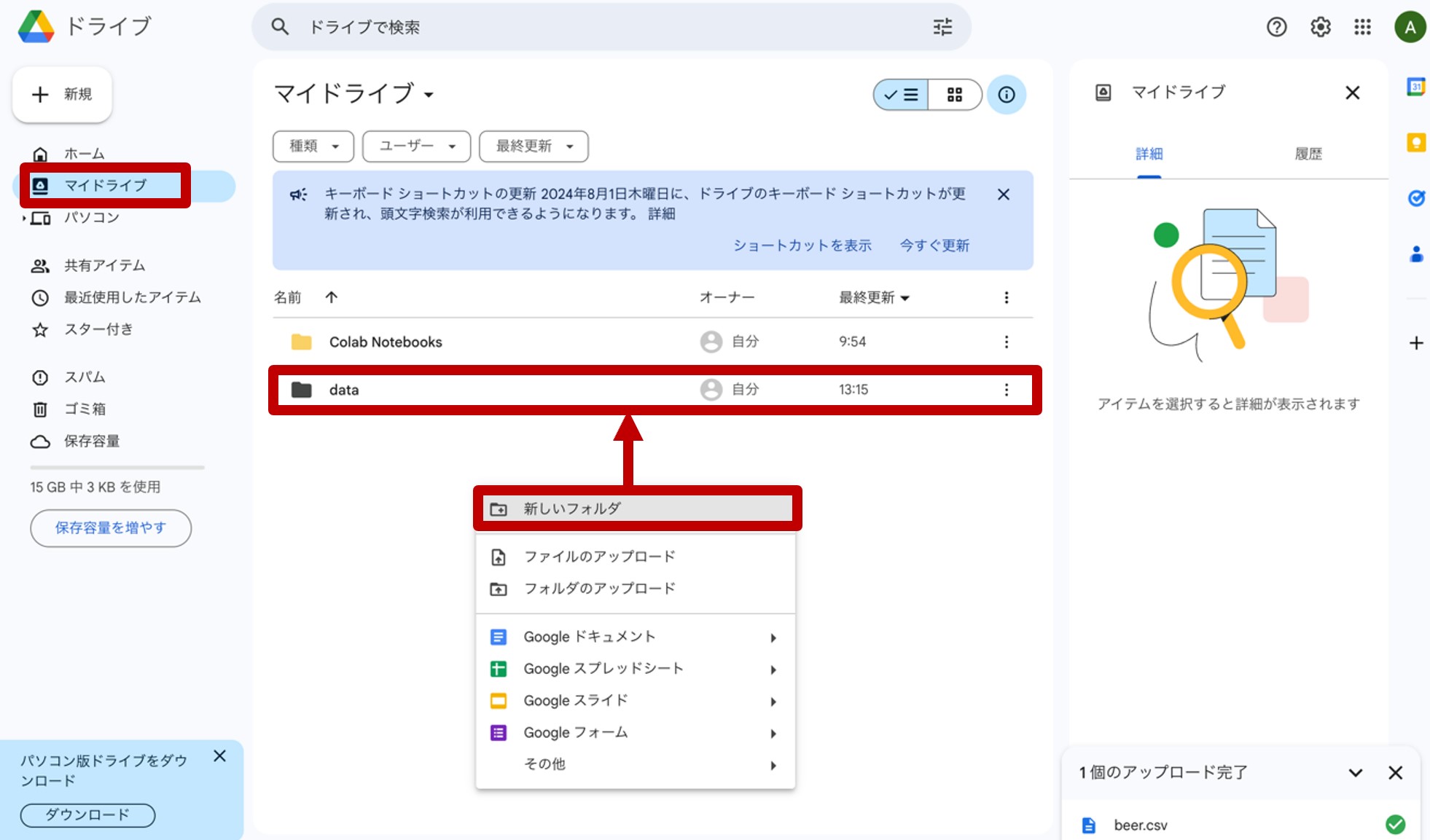
先ほどのリンクからGoogleドライブに飛び、『マイドライブ』を開きます。『マイドライブ』の空白部分を右クリックして『新しいフォルダ』を開き、「data」という名称のフォルダを作成します。(図8)

図8.マイドライブに「data」フォルダを作成

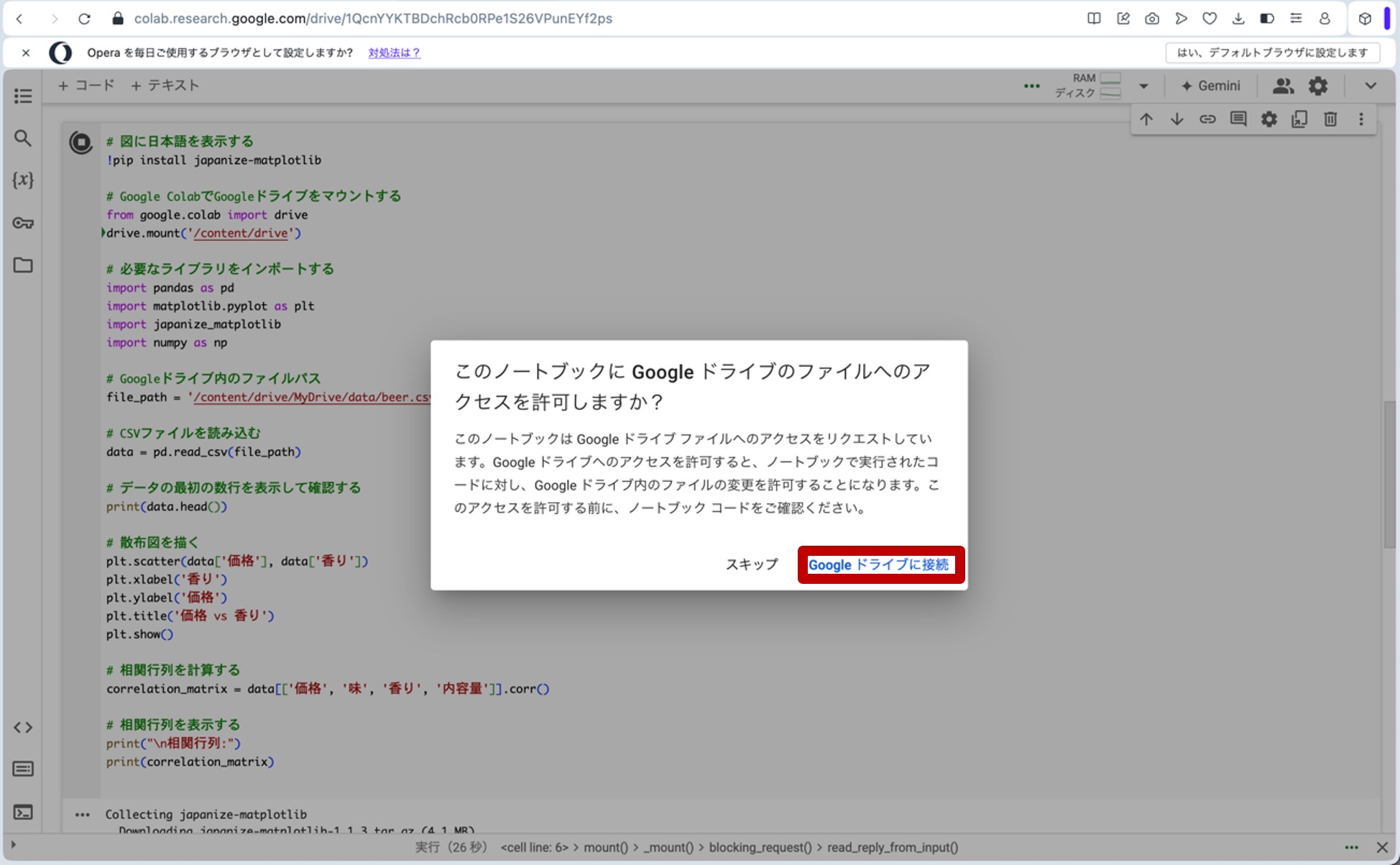
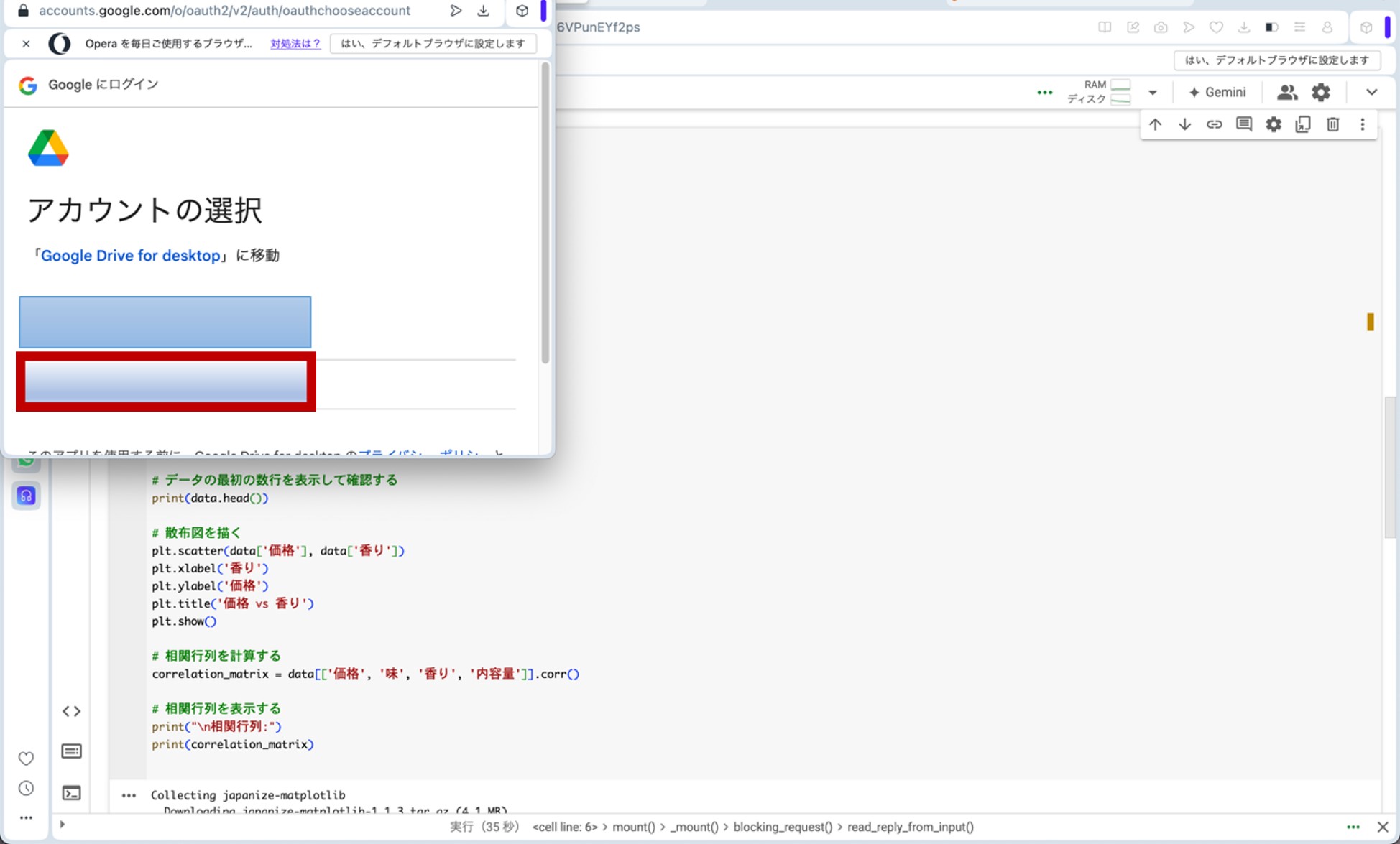
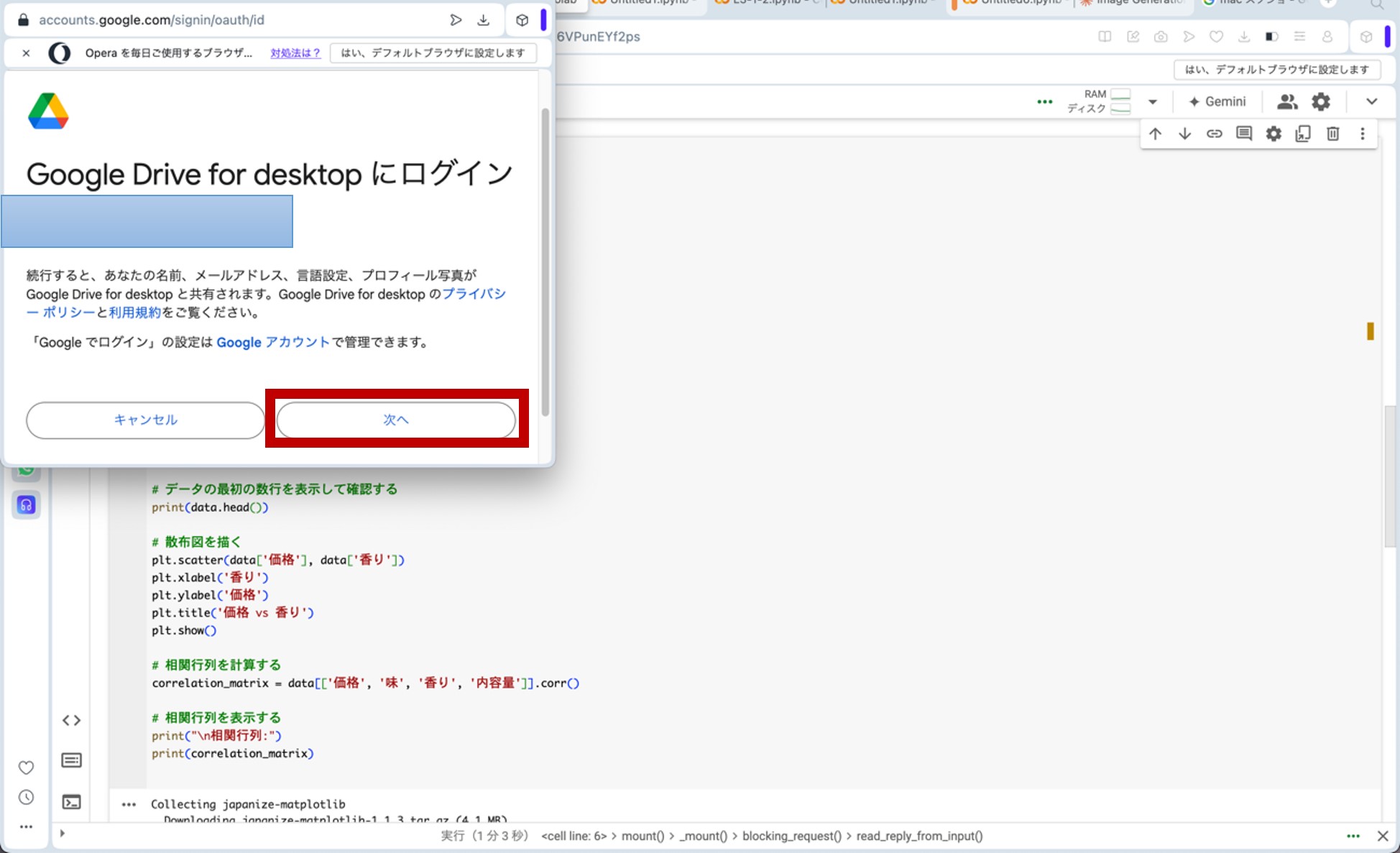
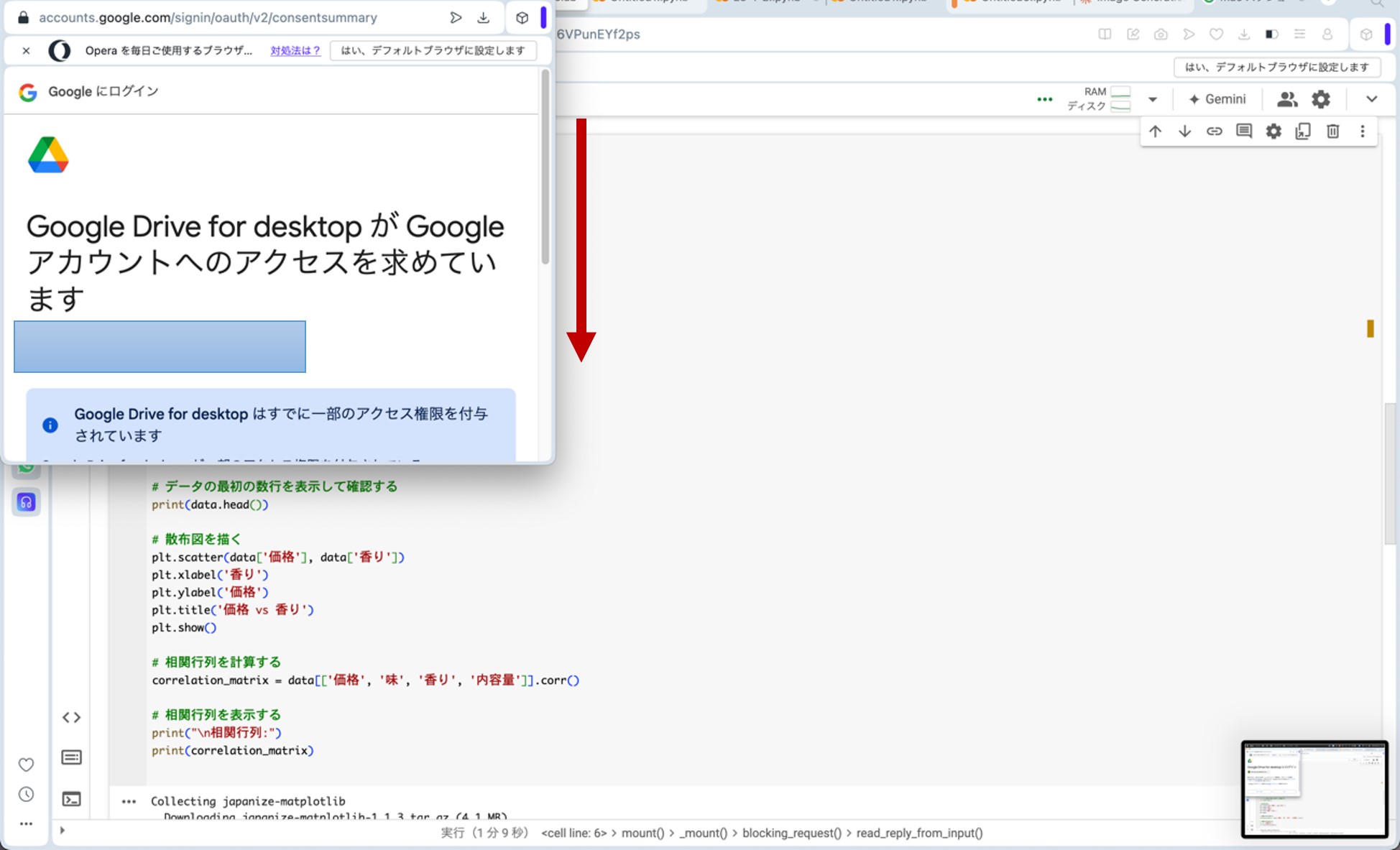
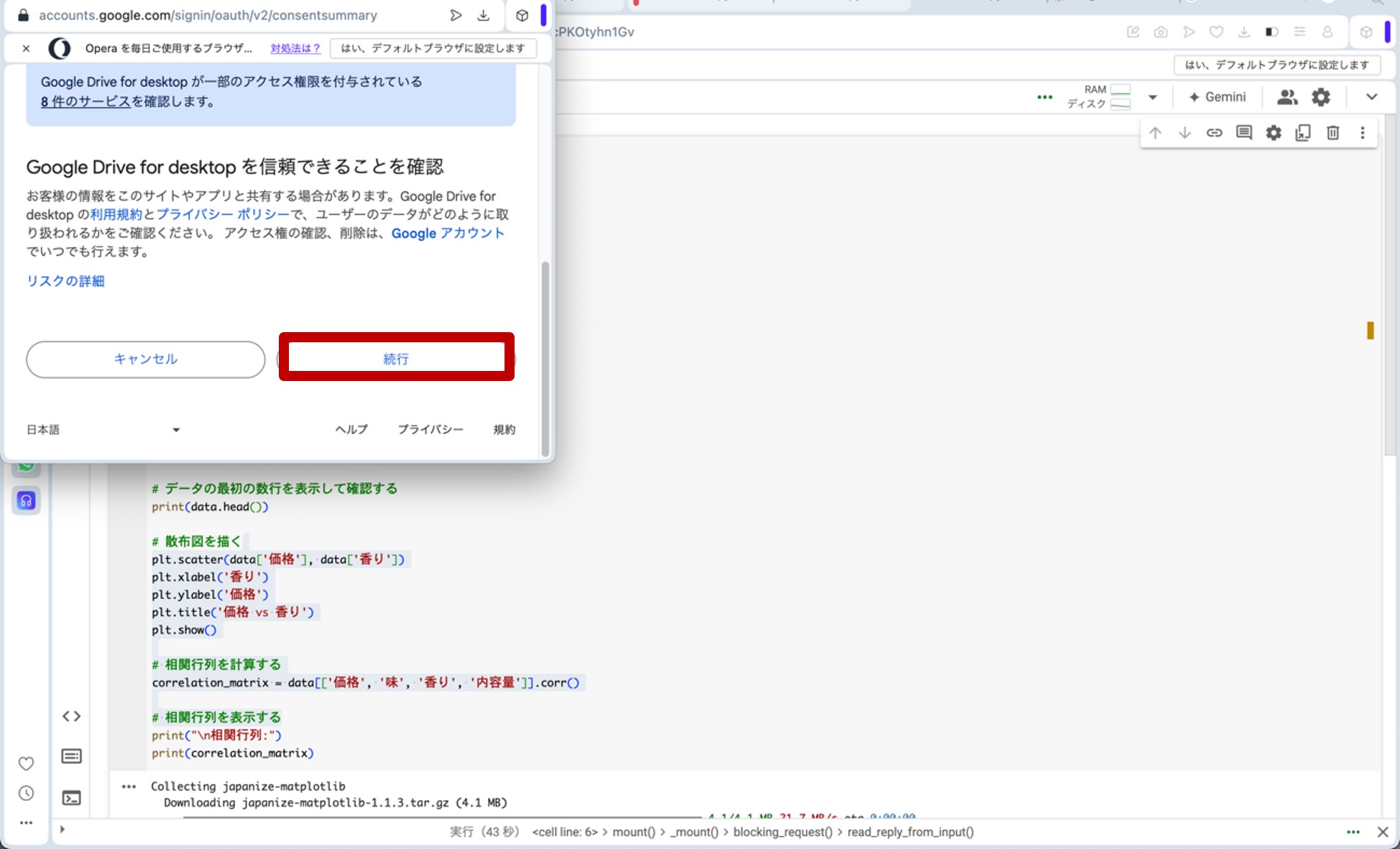
ここで、先ほどのリンクからGoogle Colaboratoryに飛びます。コードセルに以下のプログラムをコピー&ペーストし、コードセル左側にある▷ボタンを押してプログラムを走らせます。途中、ポップアップがいくつか出てきますが、図9の様に進んで下さい(『Googleドライブに接続』をクリック→自分のアカウントを選択→『次へ』をクリック→下へスクロール→『続行』をクリック)。これらの操作によって、分析に用いる架空のデータが生成されます。

図9.ポップアップへの対応

以下が、架空のデータを生成するプログラムです。

Googleドライブと連携します。

================================================================================
# Google ColabでGoogleドライブをマウント
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
#必要なライブラリをインポート
import pandas as pd
import statsmodels.api as sm
import numpy as np
================================================================================

分析用のデータを生成します。この際、毎回同じ結果が出るようにするための設定をします。

================================================================================
# ロジスティック回帰分析用のデータを生成
np.random.seed(42) # 再現性のために乱数シードを設定
n_samples = 1000
================================================================================

表形式のデータを作成します。

================================================================================
# データフレームを作成
data = {
"閲覧回数": np.random.randint(1, 100, size=n_samples),
"カートに入れた回数": np.random.randint(0, 20, size=n_samples),
"過去の購入履歴": np.random.choice([0, 1], size=n_samples),
}
================================================================================

目的変数を生成します。

================================================================================
# 目的変数を生成 (簡易的なロジスティックモデル)
coefs = np.array([0.05, 0.2, 1.5]) # 各変数の係数
intercept = -2
logits = (
coefs[0] * data["閲覧回数"] +
coefs[1] * data["カートに入れた回数"] +
coefs[2] * data["過去の購入履歴"] +
intercept
)
probabilities = 1 / (1 + np.exp(-logits))
data["購入する"] = (np.random.rand(n_samples) < probabilities).astype(int)
================================================================================

データを格納します。

================================================================================
# データフレームを作成
df = pd.DataFrame(data)
================================================================================

データをcsvファイルとしてGoogleドライブに保存します。

================================================================================
# データを保存
output_path = '/content/drive/My Drive/data/ロジスティック回帰用データ.csv'
df.to_csv(output_path, index=False)
================================================================================

データの保存が完了したら「データを保存しました」というメッセージが表示されるようにします。

================================================================================
print(f"データを保存しました: {output_path}")
================================================================================

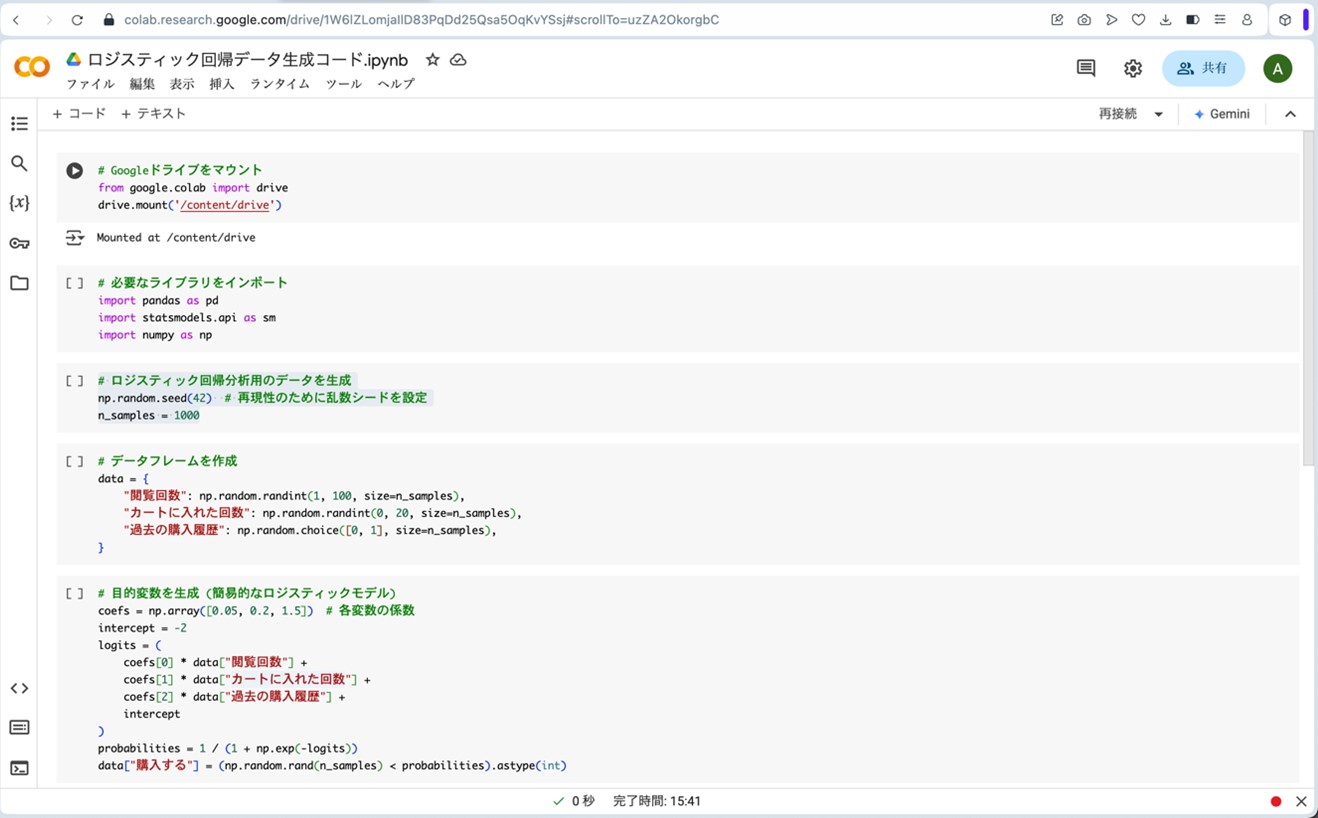
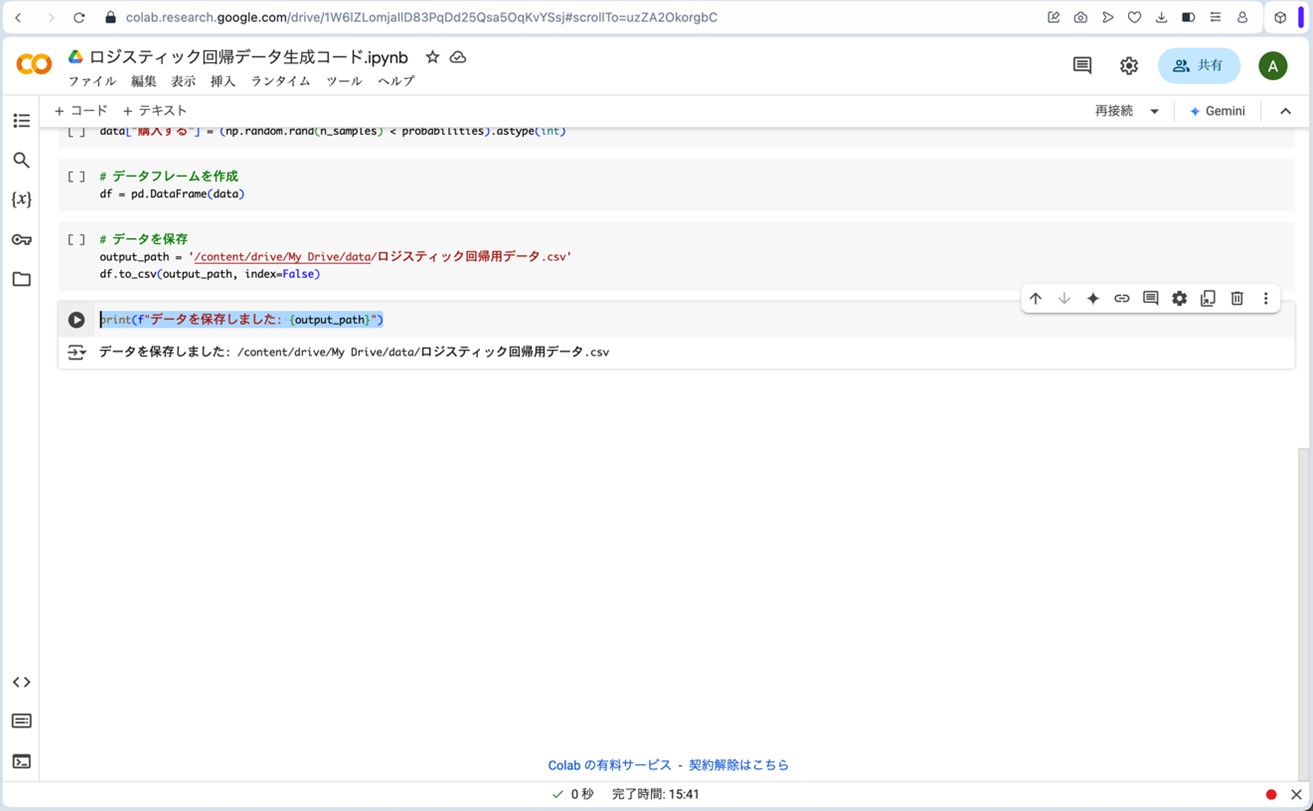
図10. Google Colaboratoryにプログラムを読み込ませて、架空のデータを生成

先ほどGoogleドライブのマイドライブ内に作成したdataフォルダをクリックしてみると、「ロジスティック回帰用データ.csv」というファイルが格納されているのが確認できます(図11)。

図11. マイドライブの「data」フォルダへ「ロジスティック回帰用データ.csv」が格納されている

次に、Google Colaboratoryに戻ります。図3〜6の手順を参考に、図7の画面まで進みます。ここで、以下のプログラムをコピーして、コードセルに貼り付けます。そして、▷ボタンを押して、プログラムを走らせると、プログラムを走らせると、ロジスティック回帰分析の結果が算出されます。

ロジスティック回帰分析のデモ分析

まずはロジスティック回帰分析のプログラムです。「ある商品を購入するか(1)、購入しないか(0)」を目的変数とし、「閲覧回数」・「カートに入れた回数」・「過去の購入履歴」を説明変数とした重回帰分析の方程式を考えます。

Googleドライブと連携します。

================================================================================
# Googleドライブをマウント
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
# 必要なライブラリのインポート
import pandas as pd
import statsmodels.api as sm
import numpy as np
================================================================================

先ほど生成したデータを読み込みます。

================================================================================
# データを読み込み
input_path = '/content/drive/My Drive/data/ロジスティック回帰用データ.csv'
df = pd.read_csv(input_path)
================================================================================

説明変数と目的変数を設定します。

================================================================================
# 説明変数と目的変数を設定
X = df[["閲覧回数", "カートに入れた回数", "過去の購入履歴"]]
y = df["購入する"]
================================================================================

定数項を追加します。

================================================================================
# 定数項を追加
X = sm.add_constant(X)
================================================================================

データに合うロジスティック回帰の計算式を作成します。

================================================================================
# ロジスティック回帰モデルを作成してフィッティング
model = sm.Logit(y, X)
result = model.fit()
================================================================================

結果を表示します。

================================================================================
# 結果を表示
print(result.summary())
================================================================================

オッズ比を計算して表示します。

================================================================================
# オッズ比を計算して表示
odds_ratios = np.exp(result.params)
print("\nオッズ比:")
print(odds_ratios)
===============================================================================

図12.サンプルプログラムでロジスティック回帰分析の結果を算出

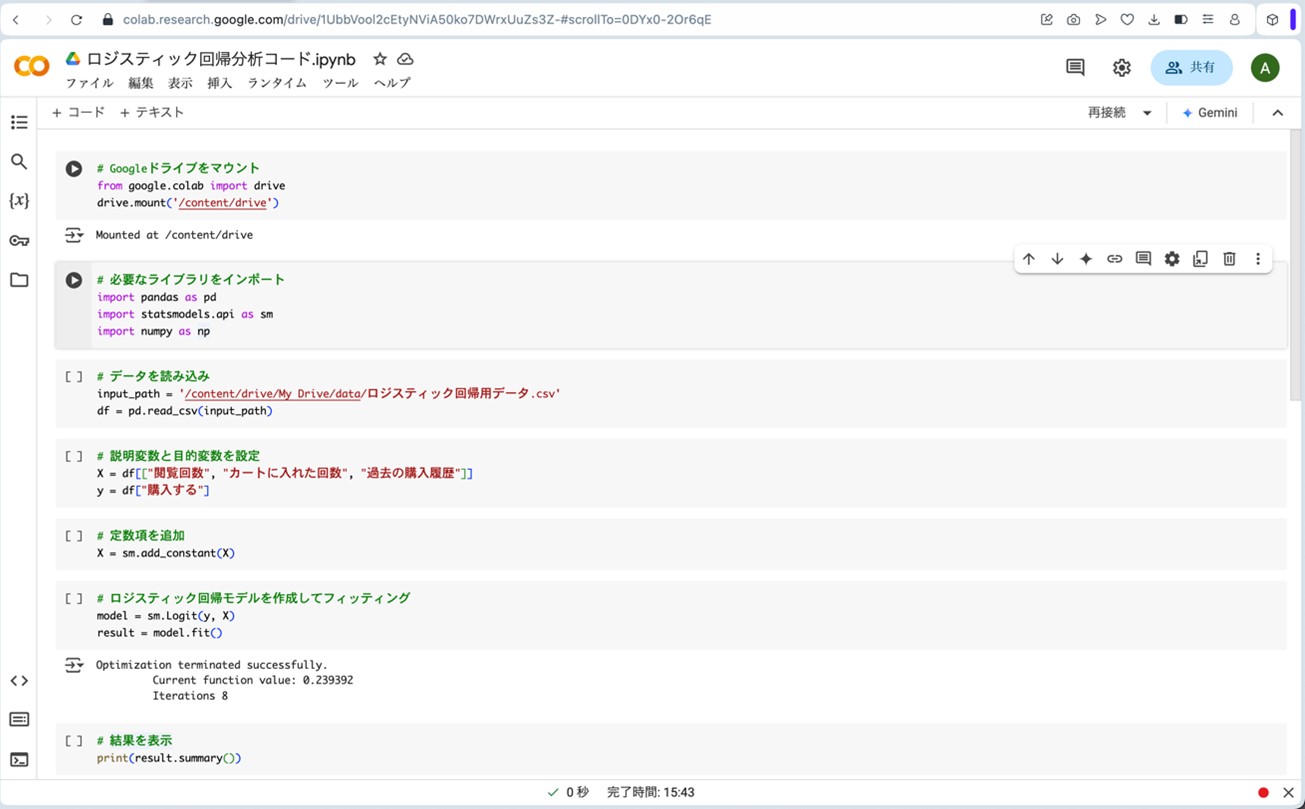
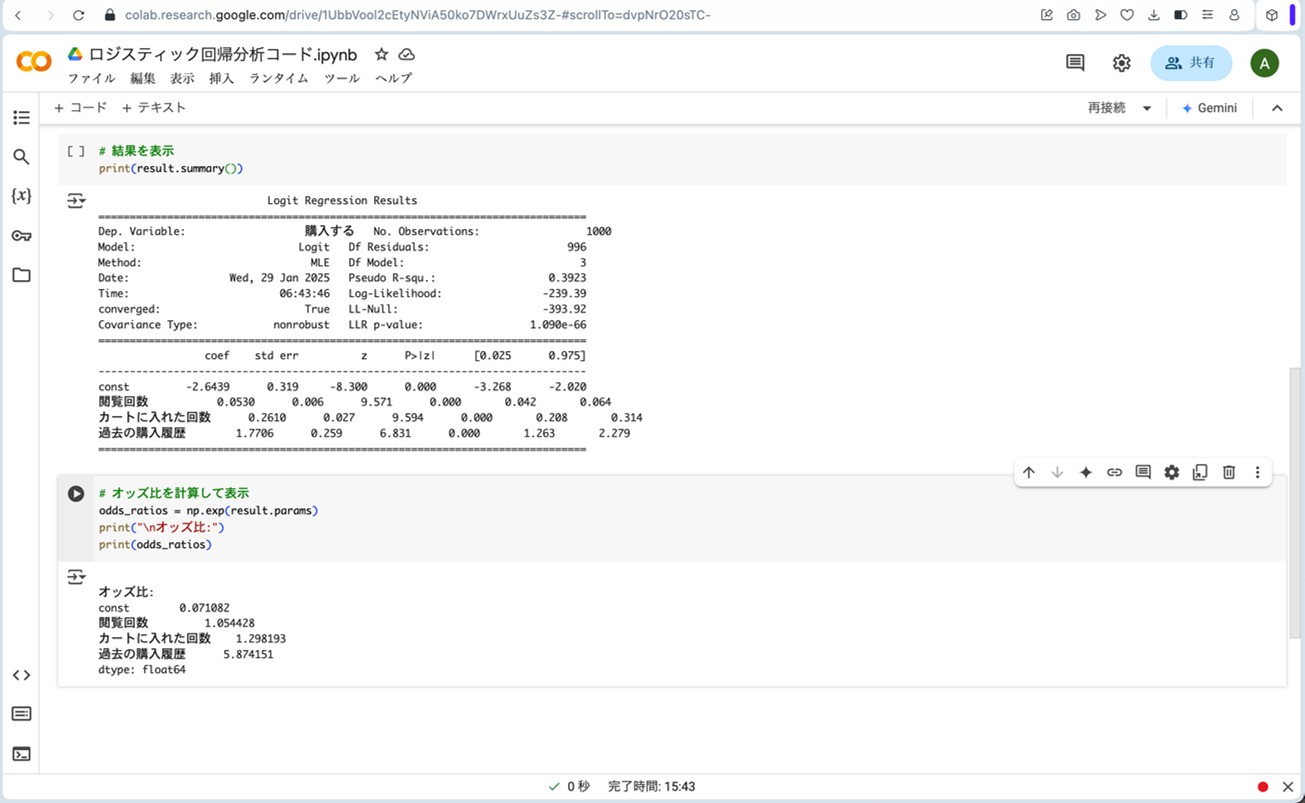
図13.拡大したロジスティック回帰分析の結果

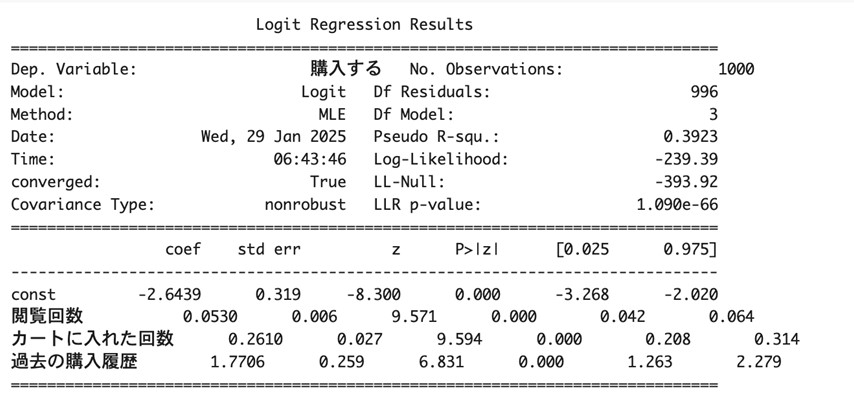
結果を解釈していきましょう。

1. 目的変数の係数のP>|z|(p値)が全て0.05以下なので、これらの係数は「統計的に意味がある」と言えます(これは数学的定義ですから、ここでは説明は割愛します。)。
2. 「閲覧回数」のオッズ比が1.054であることから、閲覧回数が1回増加すると、ある商品の購入可能性が5.4%増加します。
3. 「カートに入れた回数」のオッズ比が1.298であることから、カートに入れた回数が1回増加すると、ある商品の購入可能性が29.8%増加します。
4. 「過去の購入履歴」のオッズ比が5.874であることから、過去に、ある商品を購入したことがあるユーザーの方が、購入したことがないユーザーより、ある商品の購入可能性が5.874倍になります。

Googleドライブを利用される際はこちらをご確認、ご理解の上ご利用ください。

Google ドライブ利用規約

ドライブにおけるユーザーのプライバシー保護とユーザー自身による管理
Google ドライブ ヘルプ

※Googleドライブの説明に使用している各図は、Googleのウェブページを撮影して掲載しています。

1. 所属等は執筆当時のもので、現在とは異なる場合があります。
2. また記事中の技術、手法等については、今後の技術の進展、外部環境の変化等によっては、実情と合致しない場合があります。
3. 各記事における最新の動向につきましては、当社までぜひお問い合わせください。

著者プロフィール

プロフェッショナルズストラテジックプランニング局データソリューション部渡邉 成（わたなべ あきら）

この人の書いた記事

• 連載！データ分析②：回帰分析
• 連載！データ分析①：相関係数

得意領域

• #データアナリシス
• #機械学習
• #デジタル

著者について詳しく見る