データサイエンス 統計学 データ分析 機械学習 AI マーケティング 2025.04.08
連載！データ分析④：因子分析

因子分析とは何か？：データの背後に潜むもの

因子分析とは、多数の観測データの背後に潜む「共通の要因（因子）」を見つけ出すための統計手法です。たとえば、マーケティング場面や心理学の研究では、消費者の購買意識や性格特性を測定するために、多くの質問項目を用意します。しかし、これらの項目はすべて独立しているわけではなく、いくつかの要因によって影響を受けている可能性があります。因子分析を用いることで、それらの共通の因子を抽出し、データの構造をより簡潔に理解することができます。
因子分析の基本的な考え方は、「観測データのばらつきは、少数の因子によって説明できる」というものです。たとえば、学生の学力を評価する際に、国語や数学、理科、社会などの試験結果をもとに分析すると、「学習意欲」や「論理的思考力」といった抽象的な因子が浮かび上がるかもしれません。このように、因子分析は単なるデータの集計ではなく、データの根底にある構造を明らかにする手法なのです。
因子分析には大きく分けて「探索的因子分析」と「確認的因子分析」の2種類があります。探索的因子分析は、データの中にどのような因子が潜んでいるのかを探索する手法であり、特に研究の初期段階で有用です。一方、確認的因子分析は、事前に仮説として設定した因子構造を検証するために用いられます。どちらの手法を選択するかは、目的やデータの性質によって異なります。本章では、因子分析の入門編として、探索的因子分析について解説していきます。
因子分析はデータの背後にある共通の要因を明らかにし、複雑な情報を整理・簡略化するための重要な手法です。マーケティング、心理学、教育学、社会科学など、幅広い分野で活用されており、データをより深く理解するための鍵となる分析手法の一つといえるでしょう。

因子分析の具体的な手順

因子分析を実施するためには、いくつかのステップを順番に進めていく必要があります。以下では、一般的な因子分析の手順を説明します。

1. データの準備と前処理
   まず、分析に用いるデータを準備します。具体的には、5段階や7段階等で評定されたアンケートデータが主に用いられます。
2. 因子の抽出
   因子分析では、データから因子を抽出します。主因子法や最尤推定法などの抽出方法を用いることが一般的です。
3. 因子の回転
   因子を抽出した後、構造をより解釈しやすくするために因子回転を行います。直交回転（バリマックス回転）や斜交回転（プロマックス回転）など、目的に応じた方法を選択します。
4. 結果の解釈と考察
   最終的に、抽出された因子の意味を解釈し、目的に沿った考察を行います。因子の名称を決定し、それぞれの因子が持つ特徴や関係性を明確にします。

因子の抽出方法

因子の抽出方法には、主に「主因子法」や「最尤法」が用いられます。

1. 主因子法
   主因子法は、共通因子(複数の項目に共通する隠れた特徴)のみに焦点を当て、それらの影響を強調する手法です。この手法では、初期の因子推定において、繰り返し計算を行うことで、共通因子を抽出します。データの誤差や特異なばらつきを排除し、より単純な因子構造を得ることができます。
2. 最尤法
   最尤法は、データの分布を仮定し、その尤度(あるデータが、あるモデルに当てはまる確率の大きさ)が最大となるような因子構造を求める方法です。この手法では、因子が持つ確率的な性質を考慮するため、統計的な検定や適合度の評価が可能になります。特に、因子構造を検証したい場合に適しています。
3. その他の方法
   その他にも、最小残差法や一般化最小二乗法などと呼ばれる手法があり、目的に応じて使い分けられます。

因子の回転方法

因子の回転は、抽出された因子をより解釈しやすくするための手法です。因子分析では、因子負荷量を基に各因子の意味を解釈しますが、初期の因子抽出結果では因子の分布が複雑で理解しにくい場合があります。因子の回転を行うことで、因子負荷量の構造を単純化し、各因子の意味を明確にできます。
1．直交回転
直交回転は、因子同士が相関を持たない（独立している）ことを前提とした回転方法です。代表的な直交回転の手法には以下のようなものがあります。

1. バリマックス回転：変数が1つの因子に強く結びつき、他の因子との関連をできるだけ小さくする回転方法です。因子の解釈をシンプルにするため、最も一般的に使用されます。
2. クオーティマックス回転：各変数の因子負荷量が1つの因子に集中するように調整する回転方法で、主に全体のデータ構造を単純化する目的で使用されます。
3. エクイマックス回転：バリマックス回転とクオーティマックス回転を組み合わせた手法で、因子ごとの負荷と変数ごとの負荷のバランスを取ります。

直行回転のイメージとしては、例えば、あるバッグメーカーが、バッグA、バッグB、バッグC、バッグDの4つの異なるバックを販売したとします。4つはいずれも赤と青を使っているものの、大きさが微妙に異なるものだとします。
購入した客にアンケートを行って「気に入った箇所」を尋ねたところ、次のような結果になったとします。

図1-1.アンケートの結果

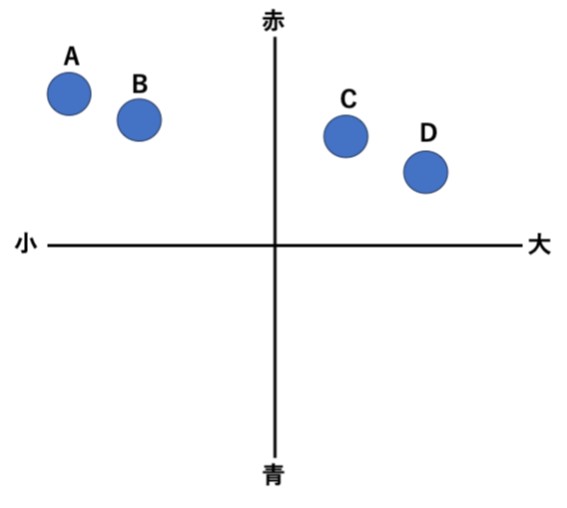
アンケート結果を上のような図にすることで、例えばバッグAは、

1. 赤い色と小さいことが客に評価された

ことが分かります。

また、この図からはそのほかにも、

1. AとBは小さいことが評価された
2. CとDは大きいことが評価された

ことが分かります。

しかし、

1. 4つのバッグはすべて赤と青を配色したが、赤と青の評価がわからない
2. AとBの顕著な違いがわからない
3. CとDの顕著な違いがわからない

ということもあげられます。
そこで、評価軸を少し回転してみます。
以下の図は、A、B、C、Dの位置は動かさず、軸全体を左に45度回転したものです。

図1-2.軸を45°回転した図

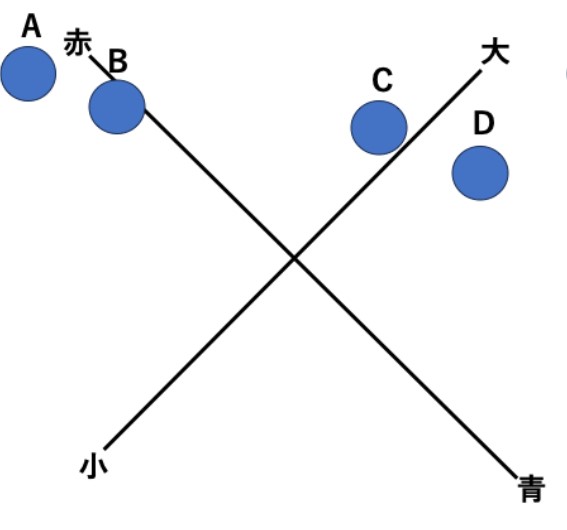
軸に注目すると「違いとして」次のことがわかります。

1. Aは赤の配色が高く評価された
2. Dは青の配色が高く評価された
3. AとBの比較では、Aの小ささとBの大きさが評価された
4. CとDの比較では、Cの赤とDの青が評価された

この内容は、元の図（軸を回転する前の図）でもよく観察すれば読み取れるのですが、軸を回転するとより素早く理解することができます(出典：ココドリ,「因子分析と軸の回転から【バリマックス回転】と【プロマックス回転】を理解する」（2025.3.15）,（https://kotodori.jp/user-research/analytics/varimax-rotation-and-promax-rotation/）)。

2．斜交回転
斜交回転は、因子間に相関がある(相互に依存関係にある)ことを許容する回転方法です。社会科学や心理学の研究では、因子が互いに影響を及ぼすことが多いため、斜交回転が適用されることがよくあります。代表的な斜交回転の手法には以下のものがあります。

1. プロマックス回転：計算が高速で、因子間に相関を持たせることが可能な回転方法です。大規模データに適しています。
2. オブリミン回転：より自由度の高い斜交回転の手法で、因子同士の相関を調整しながら最適な回転を行います。

斜交回転のイメージ図はやや複雑なので、ここでは省略します。

因子分析をやってみた

それでは、実際の因子分析について解説します。ここでは、簡易的に用意した15問のアンケートに、1000人が回答したとする架空のデータを生成して因子分析を進めていきます。これらは、後ほど実際にPythonのプログラムで実行できます。因子の抽出方法は主因子法、回転方法はバリマックス回転を選択しました。
アンケートの内容は以下です。
Q1.ブランド名を知っている
Q2.ロゴやデザインが魅力的
Q3.ブランドは信頼できる
Q4.広告は印象に残る
Q5.ターゲット層が明確
Q6.購入したいと思う
Q7.価格に見合っている
Q8.セールで購入を考える
Q9.適正価格なら選ぶ
Q10.競合と比べて納得できる
Q11.使用して満足した
Q12.友人に勧めたい
Q13.また購入したい
Q14.カスタマーサポートが良い
Q15.長期間使い続けたい
回答方法は「1.全く当てはまらない」「2.ほとんど当てはまらない」「3.あまり当てはまらない」「4.どちらでもない」「5.やや当てはまる」「6.かなり当てはまる」「7.非常に当てはまる」の7段階評定を想定しました。
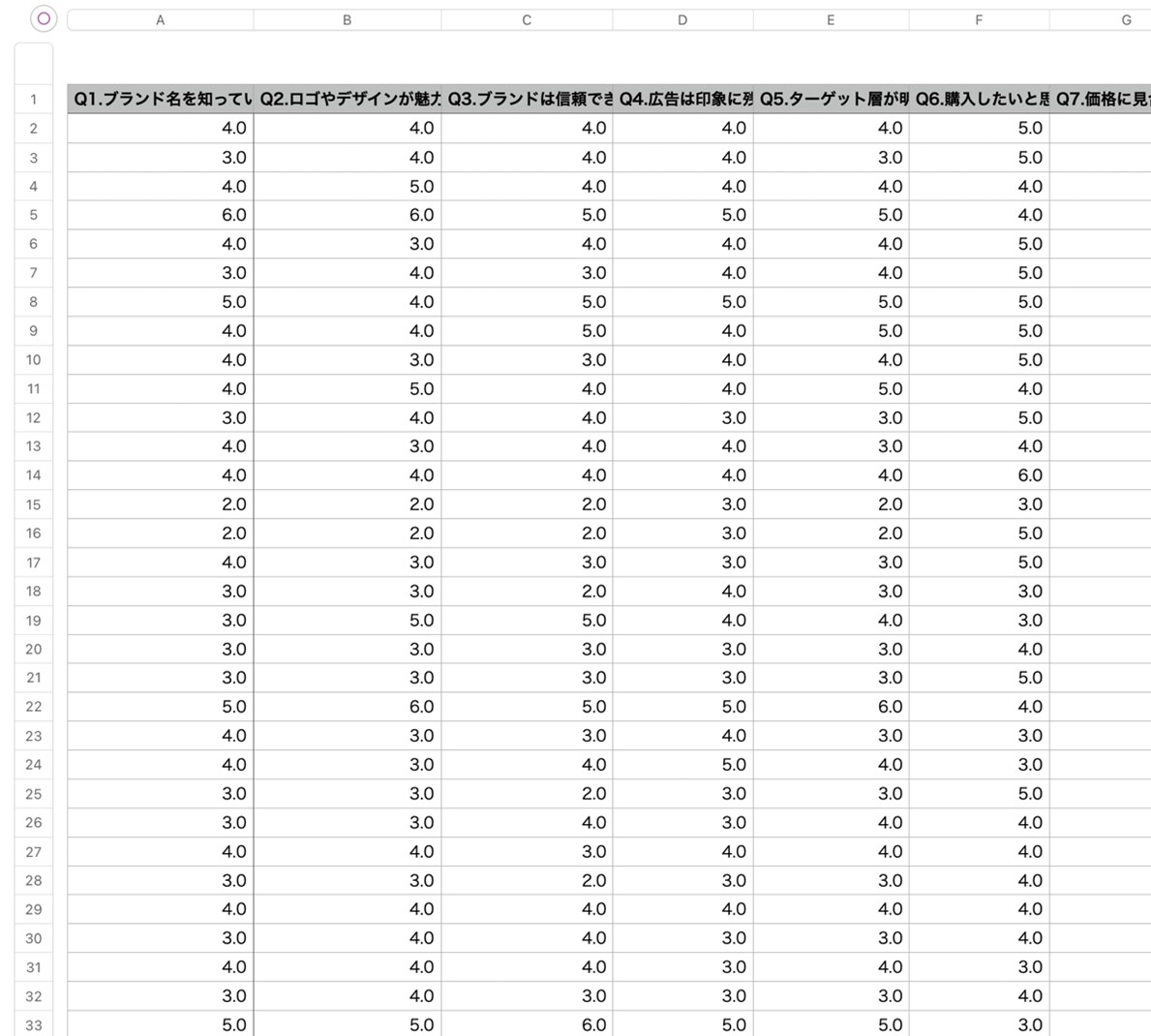
そして、このアンケートから生成した1000人分の架空の回答データは以下のようになります。

表1.アンケートデータの先頭行列

このデータを因子分析(主因子法・バリマックス回転)によって計算した結果が以下です。

表2.因子分析の結果

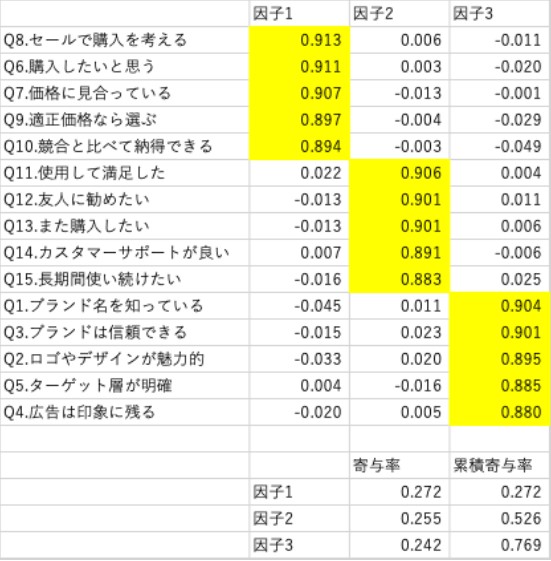
・因子負荷量と因子の命名
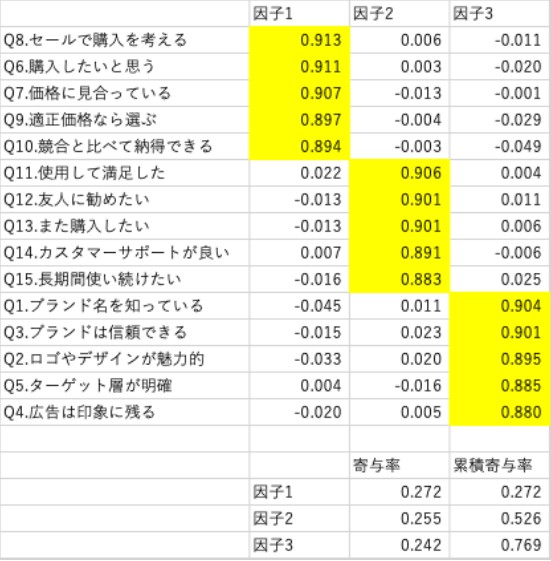
表の中に並んでいる数値は「因子負荷量」と呼ばれます。因子負荷量は、各質問項目が各因子にどれだけ関係しているかを表す値で、黄色のマーカーの部分は、他の部分に比べて非常に大きな数値となっているのが見て取れます。その結果を見て、因子構造を決定し、因子名を命名していきます。因子1は、「Q8.セールで購入を考える」「Q6.購入したいと思う」「Q7.価格に見合っている」「Q9.適正価格なら選ぶ」「Q10.競合と比べて納得できる」がまとまっているので、「価格・購入意向」因子と命名しました。因子2は、「Q11.使用して満足した」「Q12.友人に勧めたい」「Q13.また購入したい」「Q14.カスタマーサポートが良い」「Q15.長期間使い続けたい」がまとまっているので、「ブランド評価」因子と命名しました。因子3は、「Q1.ブランド名を知っている」「Q3.ブランドは信頼できる」「Q2.ロゴやデザインが魅力的」「Q5.ターゲット層が明確」「Q4.広告は印象に残る」がまとまっているので、「ブランド認知」因子と命名しました。以上のように、因子分析を使うと、複数あるアンケートデータの情報を少数の因子に縮約して簡潔に理解することができます。

・寄与率と累積寄与率
寄与率というのは、それぞれの因子がデータの何%を説明できているかを示す指標です。今回の場合では、因子１は27.2％、因子2は25.2%、因子3は24.2%、それぞれの割合でデータを説明できています。そして、それらを足し合わせると、3つの因子を合わせてデータの76.9%を説明できている、ということを表しています。累積寄与率の基準として、一般的に70~80%あれば問題ないとされることから、今回の結果は比較的当てはまりの良いものと言えます。

分析環境の構築

さて、本連載の最後には、Pythonというプログラム言語を使ってデータ分析をする方法が記載されています。それには事前準備(環境構築)が必要です。

プログラムを動かすために使用するのが、Google社の提供する、Google Colaboratory とGoogleドライブです。具体的には、Google Colaboratory 上でプログラムを動かして、Googleドライブに格納したデータを呼び出して分析する、という仕組みになっています。

以下に、その事前準備の方法を解説していきます。

Googleドライブ

まずは、Googleドライブからです。Googleのアカウントを持っている人はサインイン、Googleのアカウントを持っていない人はアカウントを作成(サインアップ)し、上記のリンクからGoogleドライブに飛んで下さい。すると、図2のようなホーム画面が出てきます。

図2.Googleドライブのホーム画面

左上の『マイドライブ』をクリックすると、図3のような画面が現れます(「Colab Notebooks」フォルダは表示されないこともありますが、今後の操作には問題ありません)。自分で入れたファイルはまだありませんが、ここに、これからの連載ごとに使用するデータを格納していきます。

図3.マイドライブの中身

画面中央下の空白(図3の赤丸部分)を右クリックして下さい。すると図4のような表示が現れます。ここから、Google Colaboratoryの設定をしていきます。

図4.Google Colaboratoryを追加

ここで、『その他』→『+アプリを追加』をクリックします。

図5.Google Colaboratoryをインストール

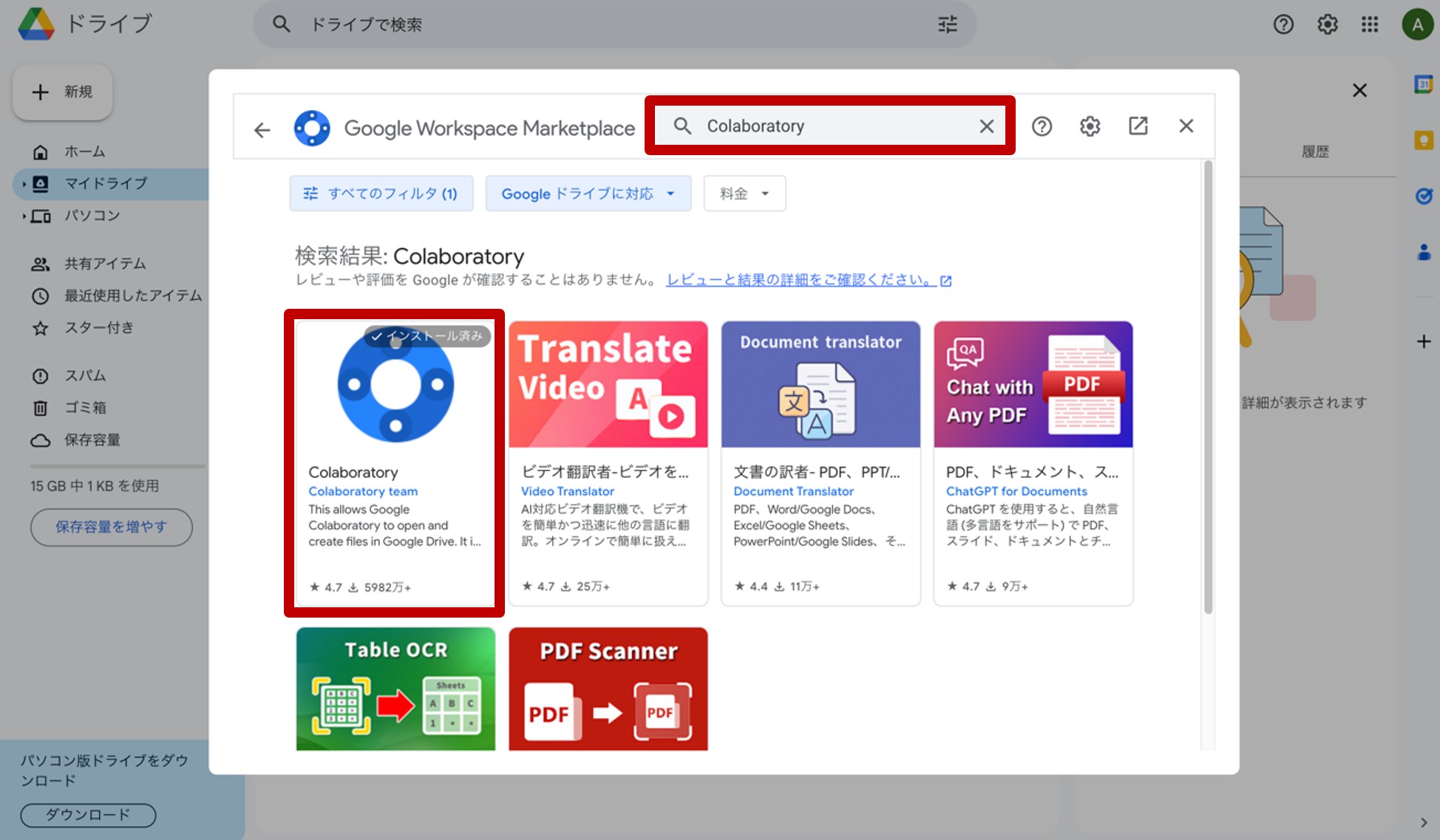
現れた画面の検索窓に『Colaboratory』と入力して検索し、インストールして下さい(図5)。以上で、Googleドライブ上での下準備は終了です。

Google Colaboratory

次に、Google Colaboratoryです。上記のリンクから飛ぶと、図6の様なホーム画面が現れます。

図6.Google Colaboratoryのホーム画面

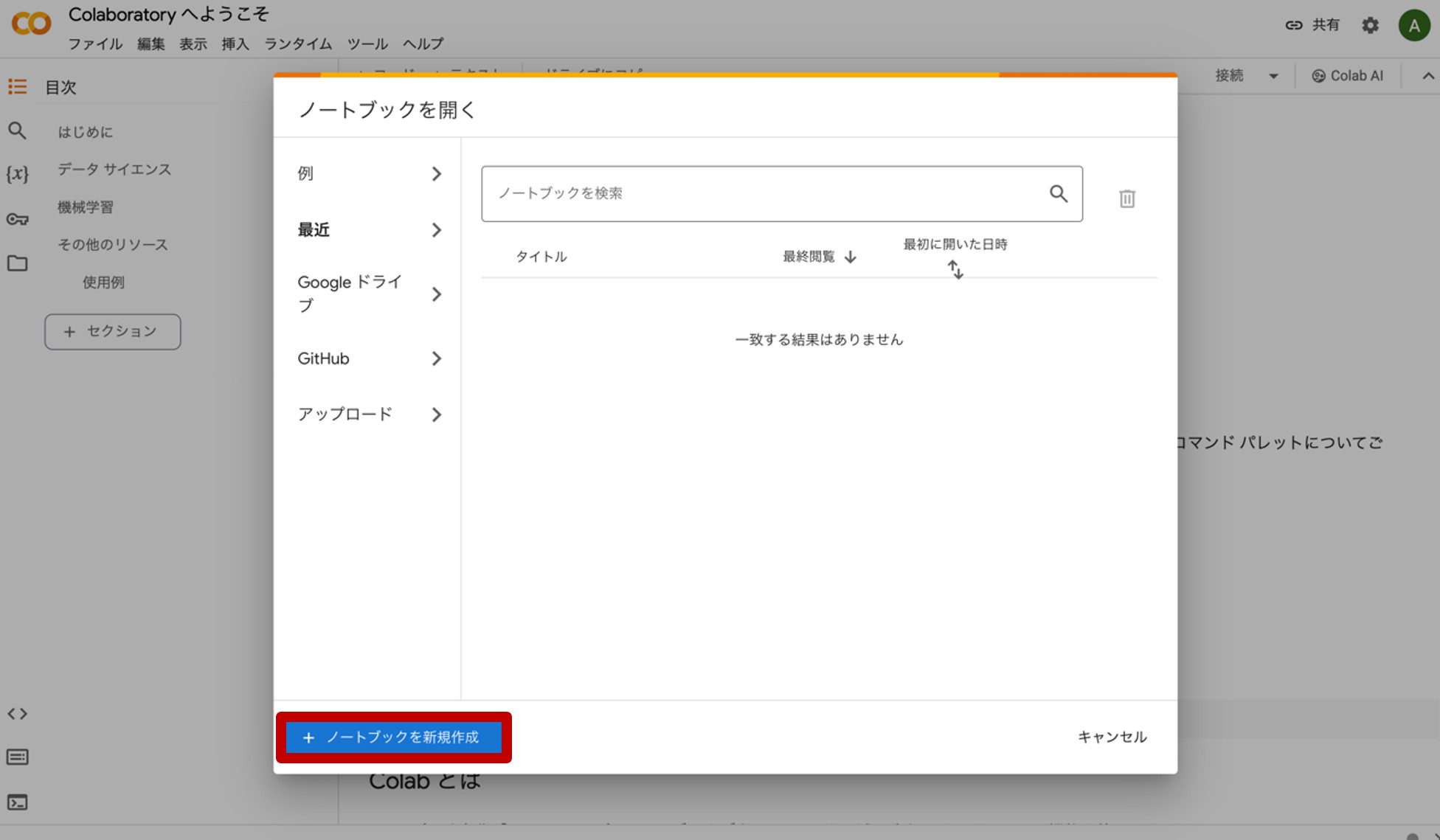
画面下側にある『ノートブックを新規作成』をクリックすると、図7のような画面が現れます。

図7.Google Colaboratoryのプログラムとテキスト入力画面

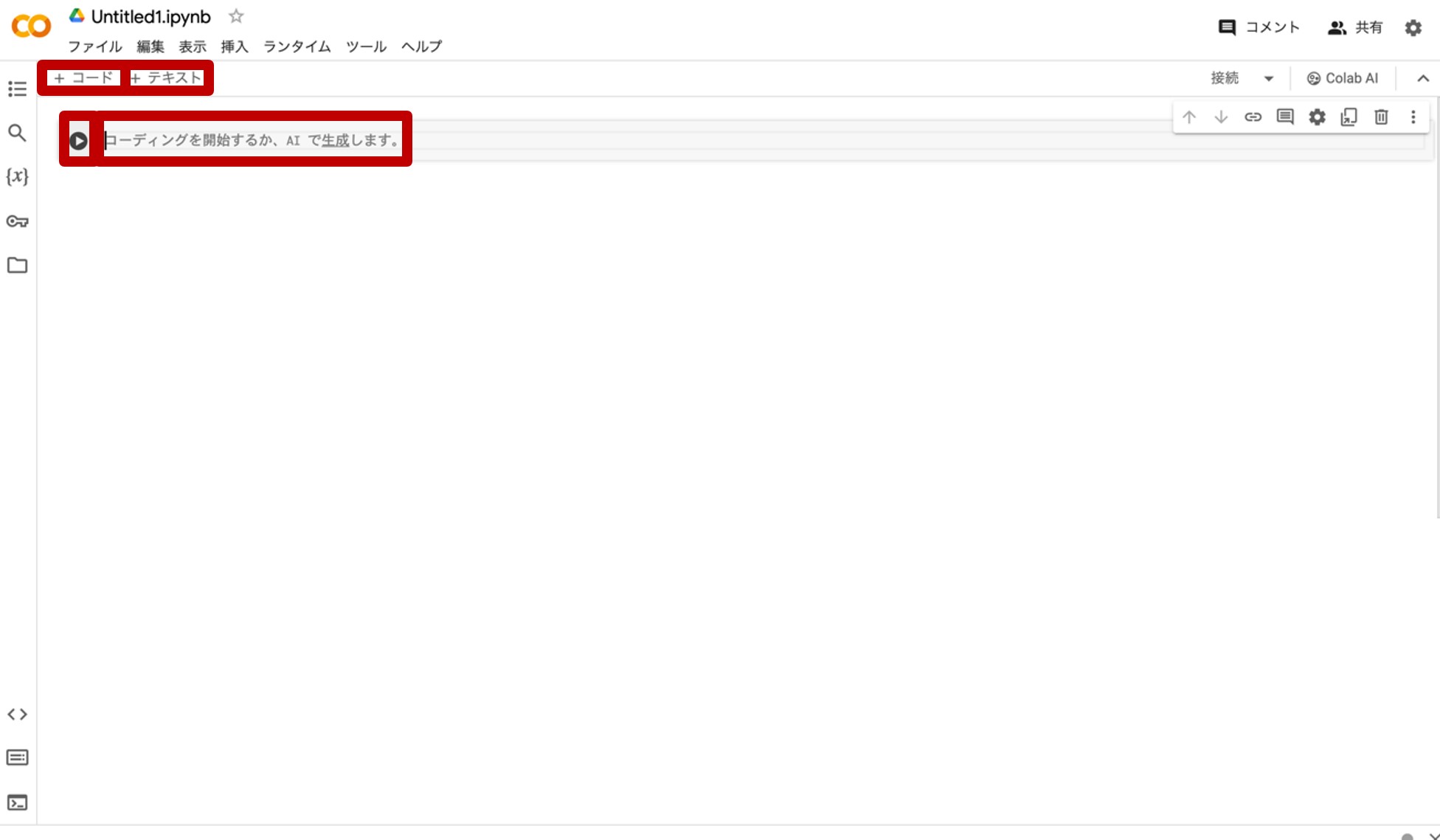
『コーディングを開始するか、AIで生成します。』(AI生成については本連載では省略します。)とあるのが、プログラムを書き込む場所であるコードセルです。左の▷ボタンを押すと当該プログラムが走り出します。分割してプログラムを書きたいときは、その上の『+コード』をクリックするとコードセルを追加することができます。
次に、『+テキスト』をクリックすると出現するのが、コードセルにあるプログラムの解説やメモを書くことができる「テキストセル」です。
以上で下準備は終了です。ここで構築した分析環境を、各連載のデモ分析の際に役立てて下さい。

実際のデータとPythonのプログラム

以下に、Pythonを用いて架空のデータを生成する方法と、因子分析を実行するPythonのプログラムを用意しています。
実際にみなさんのお手元のPCで計算して、実際の分析がどのような感覚か、まずは直感的に味わってみましょう(プログラムの文法等はひとまず置いておきましょう。)。
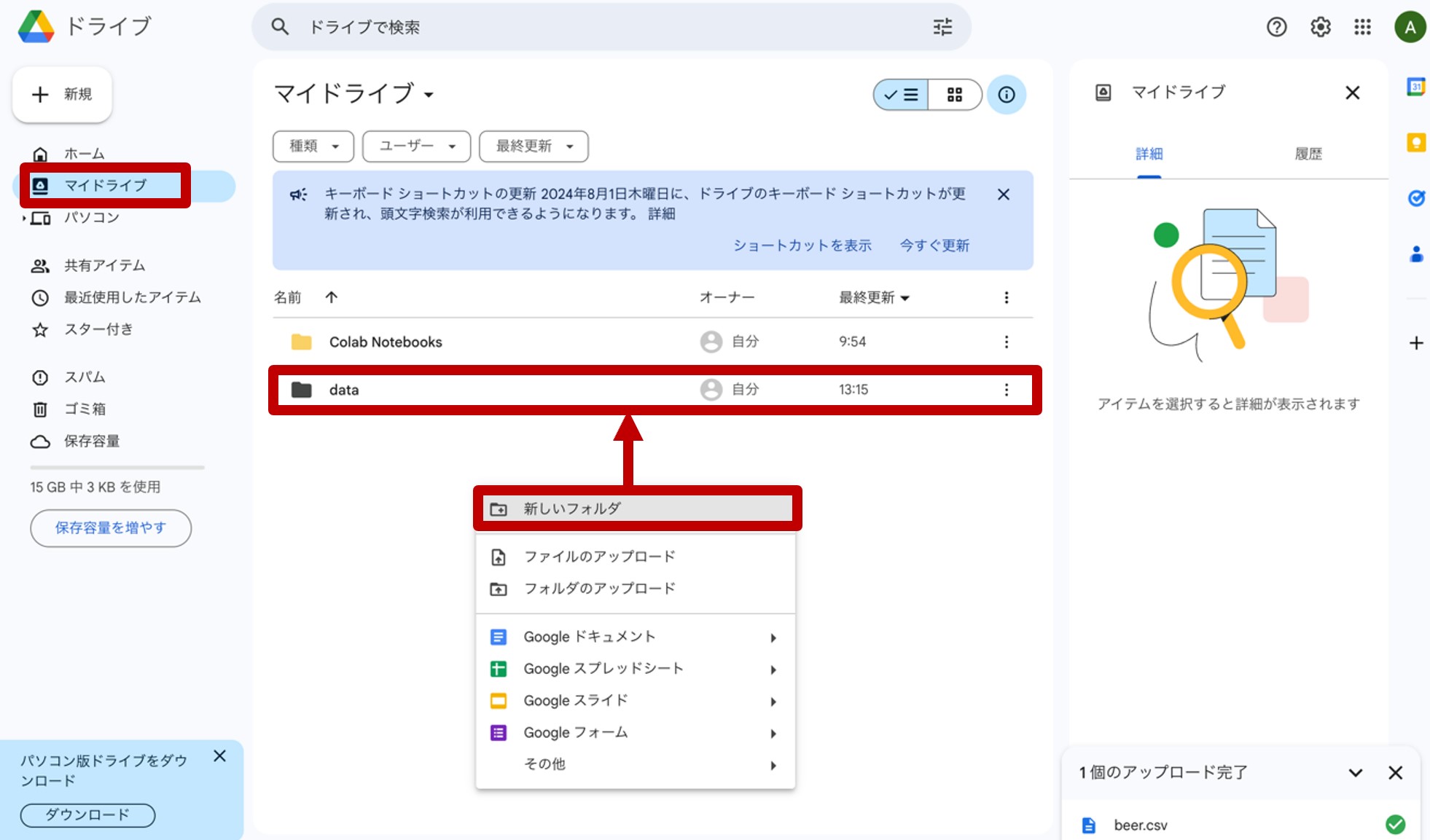
先ほどのリンクからGoogleドライブに飛び、『マイドライブ』を開きます。『マイドライブ』の空白部分を右クリックして『新しいフォルダ』を開き、「data」という名称のフォルダを作成します。(図8)

図8.マイドライブに「data」フォルダを作成

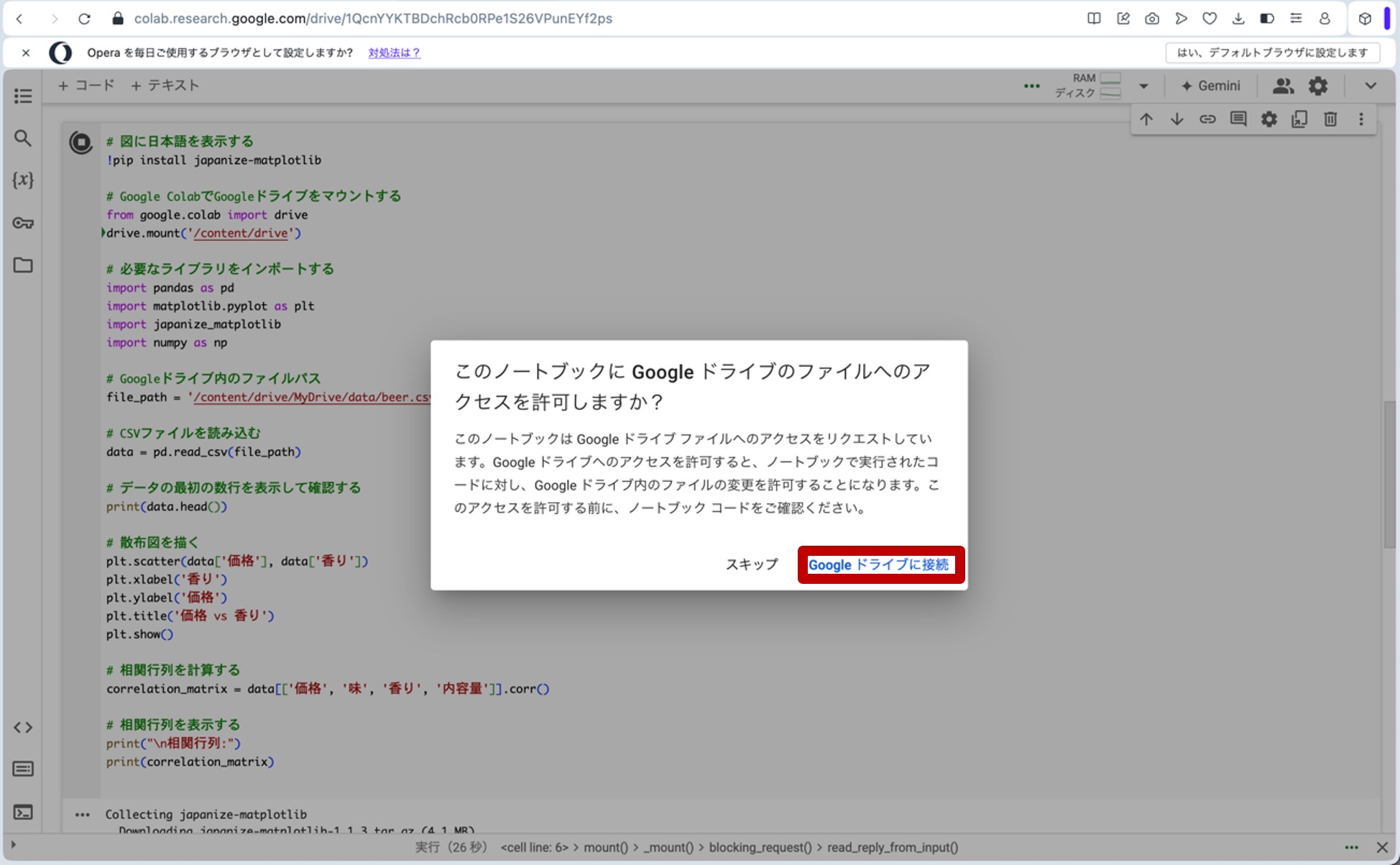
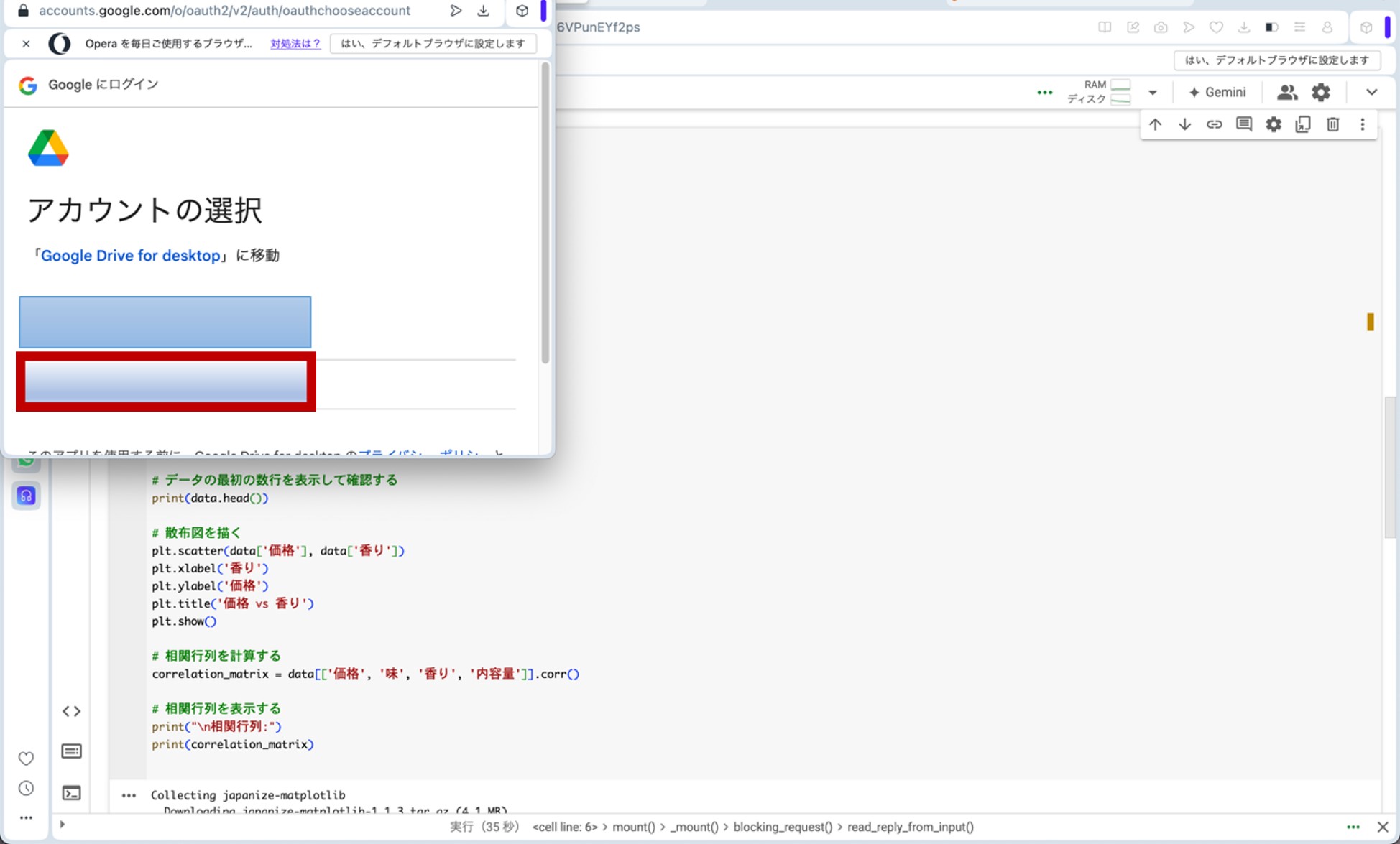
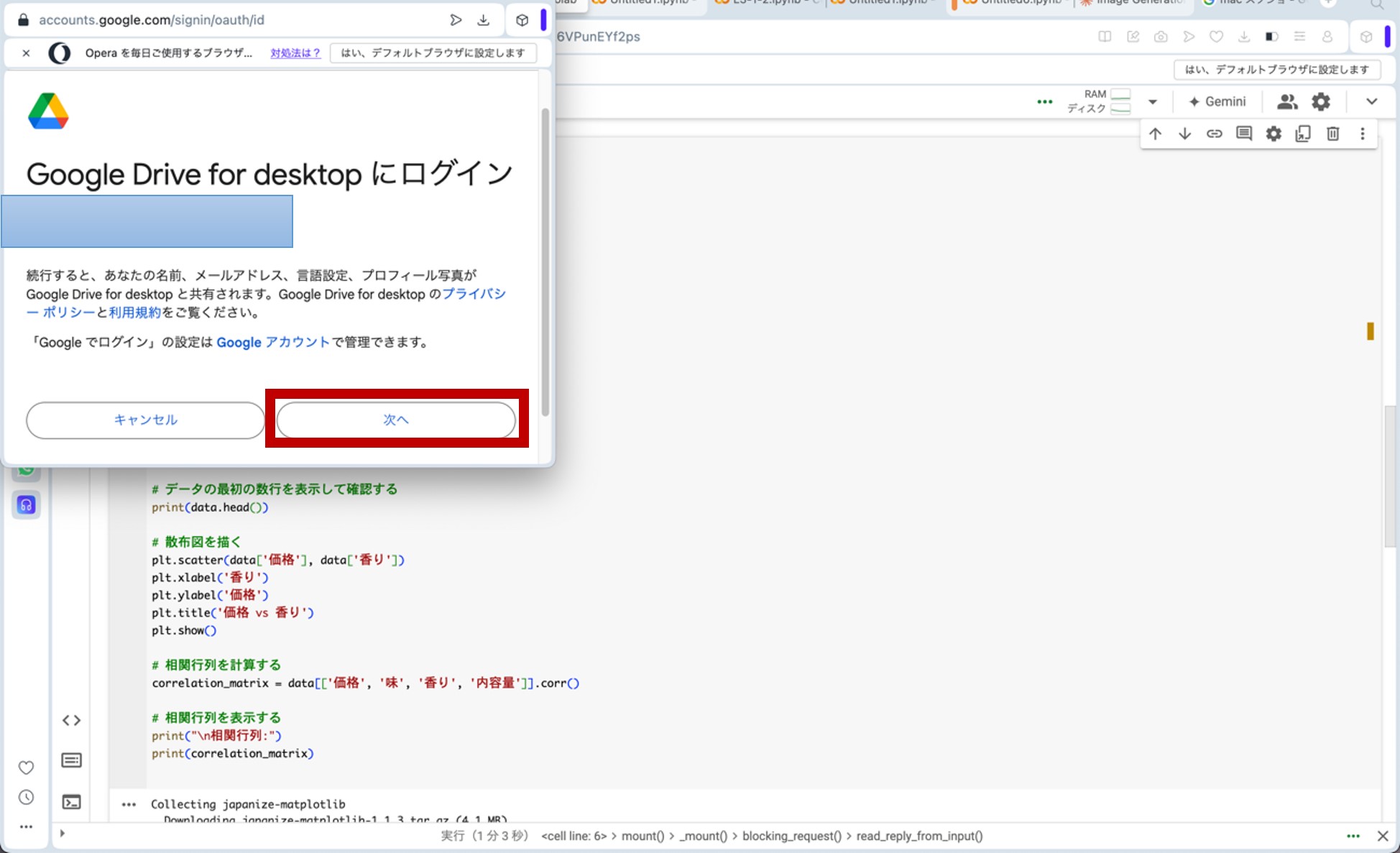
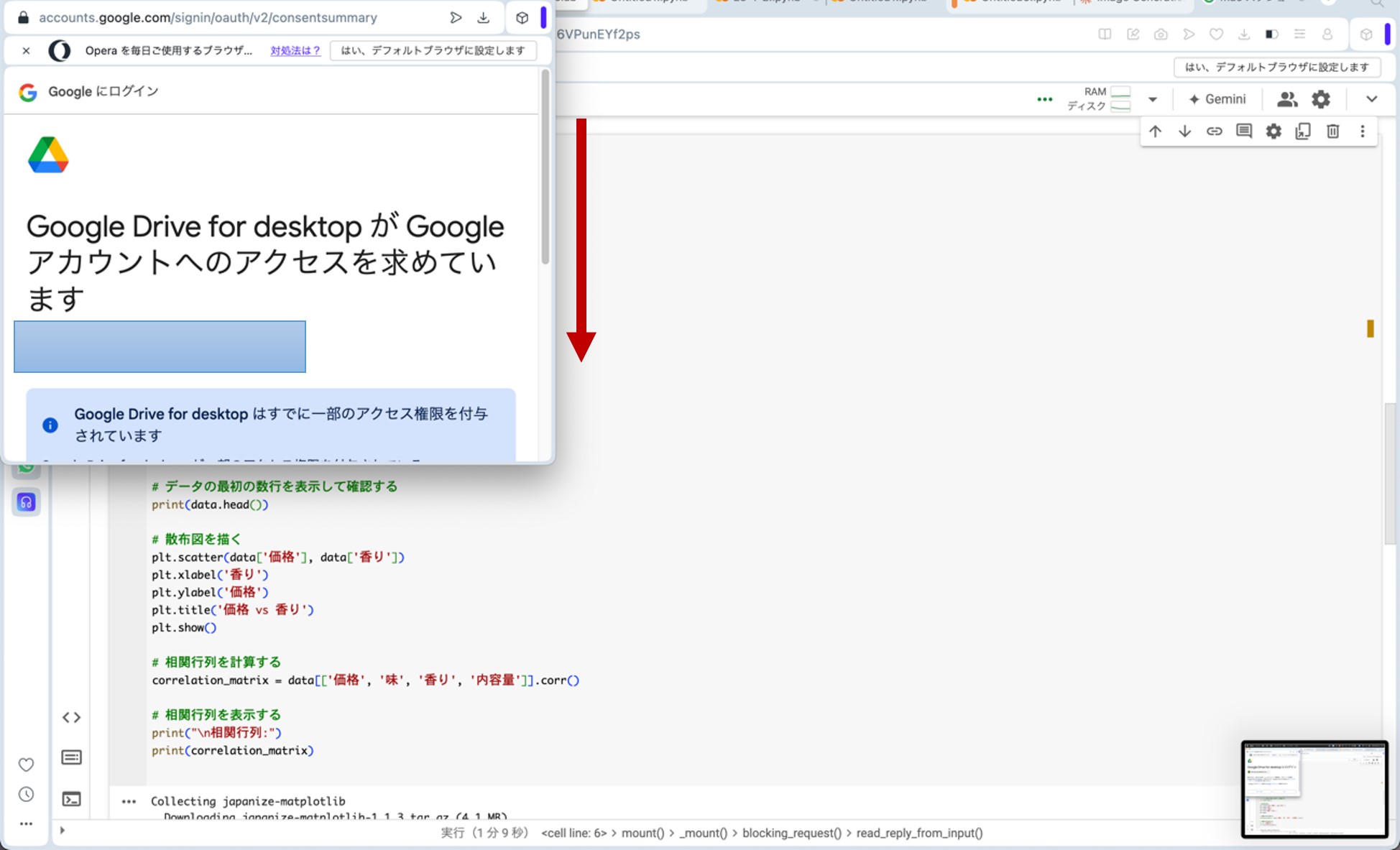
ここで、先ほどのリンクからGoogle Colaboratoryに飛びます。コードセルに以下のプログラムをコピー&ペーストし、コードセル左側にある▷ボタンを押してプログラムを走らせます。途中、ポップアップがいくつか出てきますが、図9の様に進んで下さい(「Googleドライブに接続」をクリック→自分のアカウントを選択→「次へ」をクリック→下へスクロール→「続行」をクリック)。これらの操作によって、分析に用いる架空のデータが生成されます。

図9.ポップアップへの対応

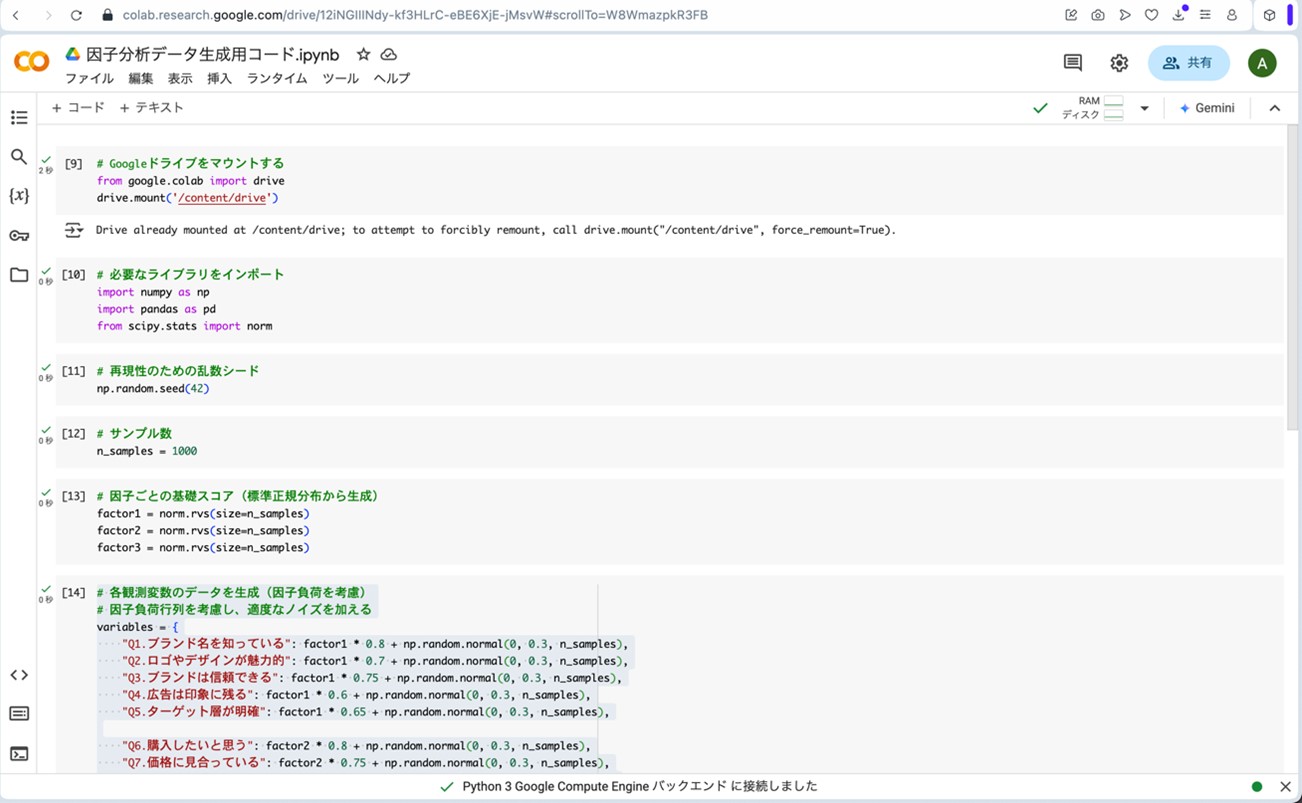
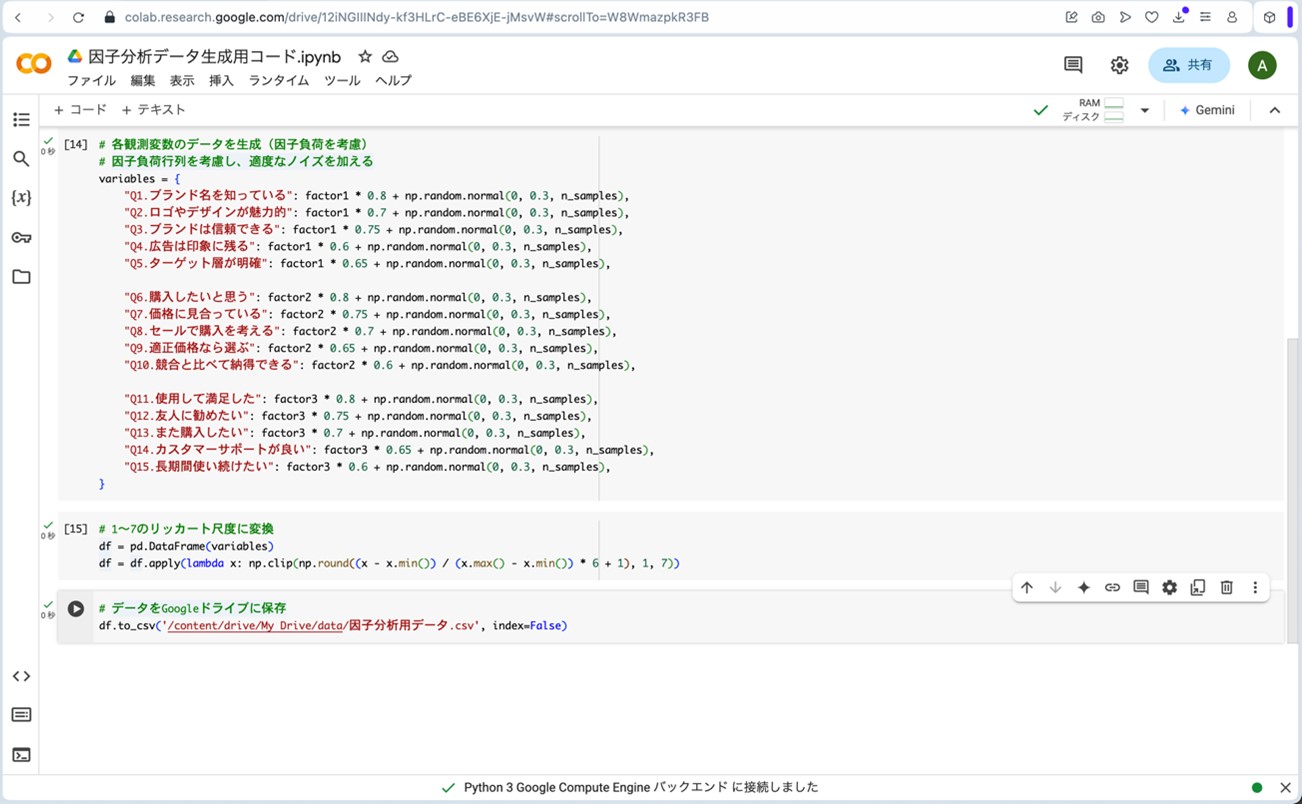
架空のデータの生成

以下が、架空のデータを生成するプログラムです。

Googleドライブと連携します。

================================================================================
# Googleドライブをマウントする
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
#必要なライブラリをインポート
import numpy as np
import pandas as pd
from scipy.stats import norm
================================================================================

何度実行しても、同じ結果が得られるように設定します。

================================================================================
# 再現性のための乱数シード
np.random.seed(42)
================================================================================

ここで生成する架空のデータのサンプル数を設定します。

================================================================================
# サンプル数
n_samples = 1000
================================================================================

各因子の基礎スコアとして、標準正規分布（平均0, 標準偏差1）からランダムにデータを生成します。

================================================================================
# 因子ごとの基礎スコア（標準正規分布から生成）
factor1 = norm.rvs(size=n_samples)
factor2 = norm.rvs(size=n_samples)
factor3 = norm.rvs(size=n_samples)
================================================================================

各因子(観測変数)のデータを、因子負荷量を考慮しつつ、適度なノイズを与えながら生成します。

================================================================================
# 各観測変数のデータを生成（因子負荷を考慮）
# 因子負荷行列を考慮し、適度なノイズを加える
variables = {
"Q1.ブランド名を知っている": factor1 * 0.8 + np.random.normal(0, 0.3, n_samples),
"Q2.ロゴやデザインが魅力的": factor1 * 0.7 + np.random.normal(0, 0.3, n_samples),
"Q3.ブランドは信頼できる": factor1 * 0.75 + np.random.normal(0, 0.3, n_samples),
"Q4.広告は印象に残る": factor1 * 0.6 + np.random.normal(0, 0.3, n_samples),
"Q5.ターゲット層が明確": factor1 * 0.65 + np.random.normal(0, 0.3, n_samples),

"Q6.購入したいと思う": factor2 * 0.8 + np.random.normal(0, 0.3, n_samples),
"Q7.価格に見合っている": factor2 * 0.75 + np.random.normal(0, 0.3, n_samples),
"Q8.セールで購入を考える": factor2 * 0.7 + np.random.normal(0, 0.3, n_samples),
"Q9.適正価格なら選ぶ": factor2 * 0.65 + np.random.normal(0, 0.3, n_samples),
"Q10.競合と比べて納得できる": factor2 * 0.6 + np.random.normal(0, 0.3, n_samples),

"Q11.使用して満足した": factor3 * 0.8 + np.random.normal(0, 0.3, n_samples),
"Q12.友人に勧めたい": factor3 * 0.75 + np.random.normal(0, 0.3, n_samples),
"Q13.また購入したい": factor3 * 0.7 + np.random.normal(0, 0.3, n_samples),
"Q14.カスタマーサポートが良い": factor3 * 0.65 + np.random.normal(0, 0.3, n_samples),
"Q15.長期間使い続けたい": factor3 * 0.6 + np.random.normal(0, 0.3, n_samples),
}
================================================================================

7段階の評定方法を指定します。

================================================================================
# 1～7のリッカート尺度に変換
df = pd.DataFrame(variables)
df = df.apply(lambda x: np.clip(np.round((x - x.min()) / (x.max() - x.min()) * 6 + 1), 1, 7))
================================================================================

データをGoogleドライブに保存します。
================================================================================
# データをGoogleドライブに保存
df.to_csv('/content/drive/My Drive/data/因子分析用データ.csv', index=False)
================================================================================

図10. Google Colaboratoryにプログラムを読み込ませて、架空のデータを生成

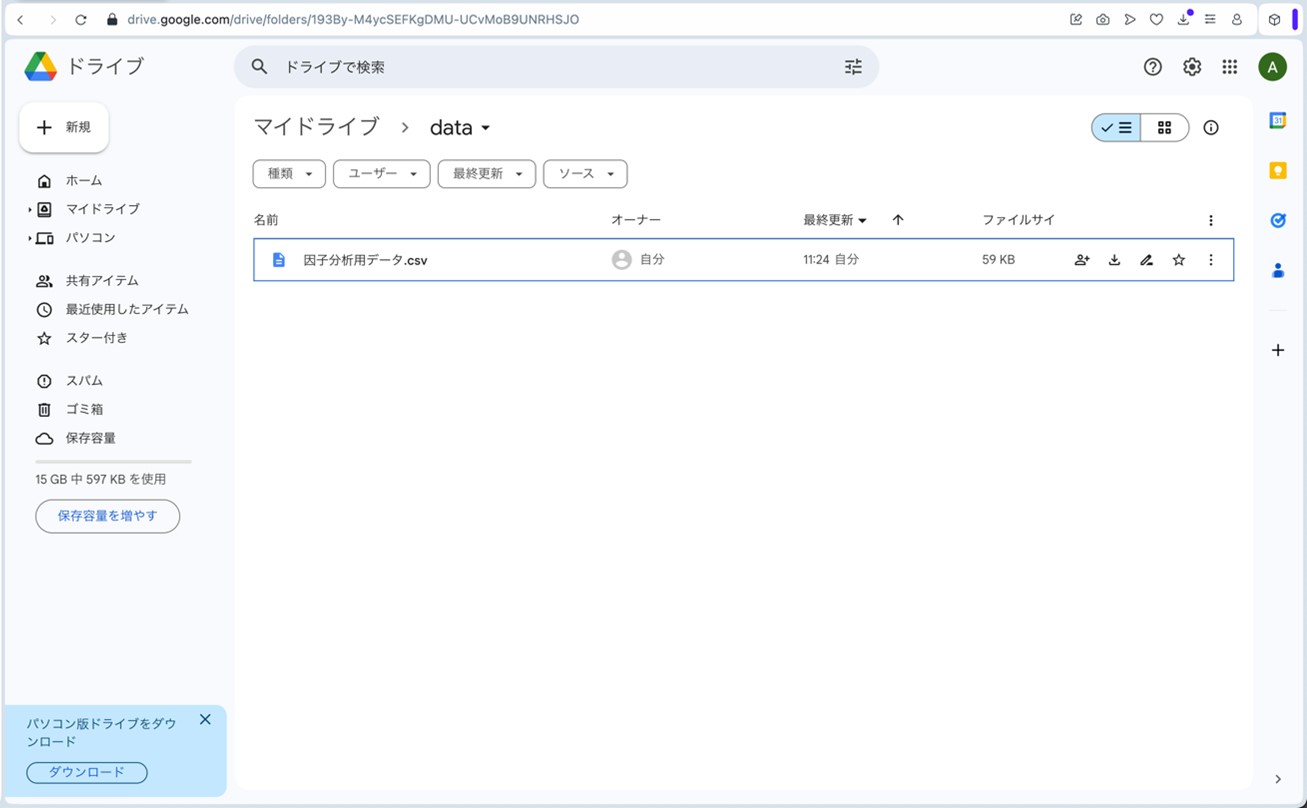
先ほどGoogleドライブのマイドライブ内に作成したdataフォルダをクリックしてみると、「因子分析用データ.csv」というファイルが格納されているのが確認できます(図11)。

図11. マイドライブの「data」フォルダへ「因子分析用データ.csv」が格納されている

次に、Google Colaboratoryに戻ります。図3〜6の手順を参考に、図7の画面まで進みます。ここで、以下のプログラムをコピーして、コードセルに貼り付けます。そして、▷ボタンを押して、プログラムを走らせると、プログラムを走らせると、因子分析の結果が算出されます。

因子分析のデモ分析

それでは、因子分析のデモ分析をPythonで行っていきましょう。
ここでは、先述の「因子分析をやってみた」の項での因子分析の結果を実際に求めていきます。簡易的に用意した15問のアンケートに、1000人が回答したとする架空のデータを生成して因子分析を進めていきます。データは先ほどすでに生成してあるので、それを使って分析していきます。因子の抽出方法は主因子法、回転方法はバリマックス回転を選択しました。
アンケートの内容は以下です。
Q1.ブランド名を知っている
Q2.ロゴやデザインが魅力的
Q3.ブランドは信頼できる
Q4.広告は印象に残る
Q5.ターゲット層が明確
Q6.購入したいと思う
Q7.価格に見合っている
Q8.セールで購入を考える
Q9.適正価格なら選ぶ
Q10.競合と比べて納得できる
Q11.使用して満足した
Q12.友人に勧めたい
Q13.また購入したい
Q14.カスタマーサポートが良い
Q15.長期間使い続けたい
回答方法は「1.全く当てはまらない」「2.ほとんど当てはまらない」「3.あまり当てはまらない」「4.どちらでもない」「5.やや当てはまる」「6.かなり当てはまる」「7.非常に当てはまる」の7段階評定を想定しました。
以下が因子分析のプログラムです。


Googleドライブと連携します。

================================================================================
# Googleドライブをマウント
from google.colab import drive
drive.mount('/content/drive')
================================================================================

必要なライブラリをインポートします。

================================================================================
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
from scipy.stats import zscore
================================================================================

必要なライブラリをインポートします。

================================================================================
# 必要なライブラリをインストール
!pip install factor-analyzer
from factor_analyzer import FactorAnalyzer
================================================================================

Googleドライブから先ほど生成したデータを読み込みます。

================================================================================
# Google Drive からデータを読み込む
df = pd.read_csv('/content/drive/My（ Drive/data/因子分析用データ.csv')
================================================================================

データを標準化(-1~1の相対的な値にすること)します。

================================================================================
# 標準化
df_standardized = df.apply(zscore)
================================================================================

因子抽出方法は主因子法、因子の回転方法はバリマックス回転で因子分析を実行します。

================================================================================
# 因子分析（主因子法 + バリマックス回転）
fa = FactorAnalyzer(n_factors=3, method='principal', rotation='varimax')
fa.fit(df_standardized)
================================================================================

因子負荷量を取得します。

================================================================================
# 因子負荷量を取得
loadings = pd.DataFrame(fa.loadings_, index=df.columns, columns=["因子1", "因子2", "因子3"])
================================================================================

データの特徴を表す数値（固有値）を取り出す。

================================================================================
# 固有値を取得
eigenvalues, variance = fa.get_eigenvalues()
================================================================================

全体のばらつきに対する各因子の割合(寄与率)を計算します。

================================================================================
# 総分散で正規化して寄与率を計算
total_variance = sum(eigenvalues)
explained_variance_ratio = variance[:3] / total_variance # 正規化された寄与率
cumulative_variance_ratio = np.cumsum(explained_variance_ratio) # 累積寄与率
================================================================================

結果を表示します。

================================================================================
# 結果を表示
print("因子負荷量:")
print(loadings)
print("\n寄与率と累積寄与率:")
contribution_df = pd.DataFrame({"寄与率": explained_variance_ratio, "累積寄与率": cumulative_variance_ratio}, index=["因子1", "因子2", "因子3"])
print(contribution_df)
================================================================================

図12.サンプルプログラムで因子分析の結果を算出

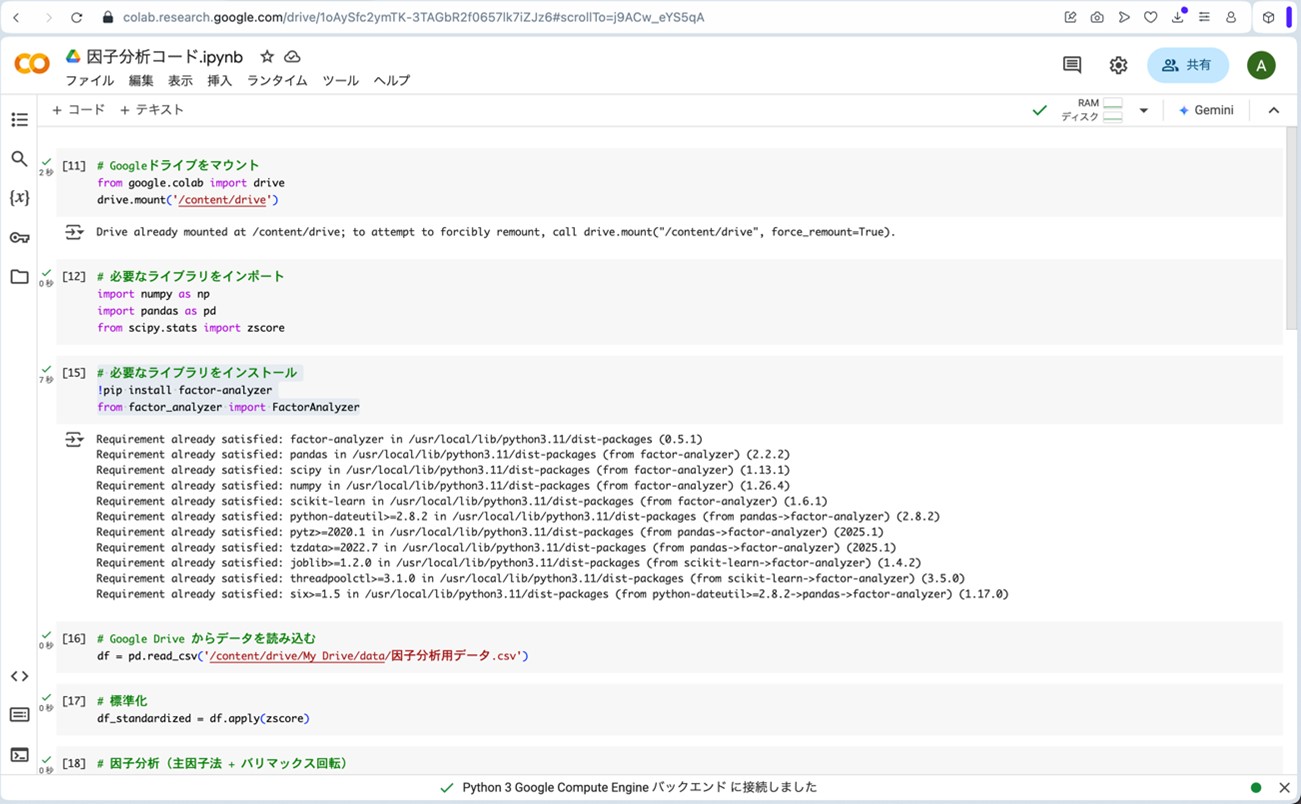
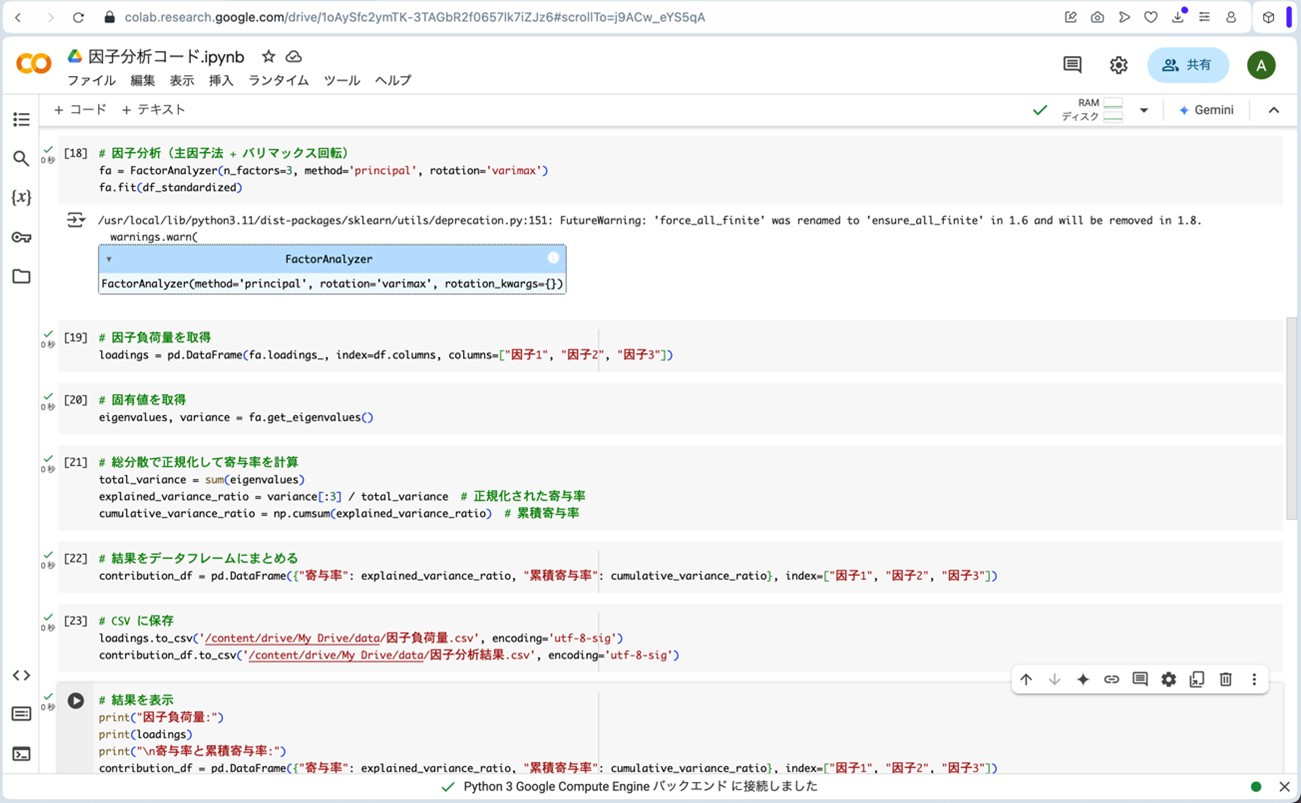
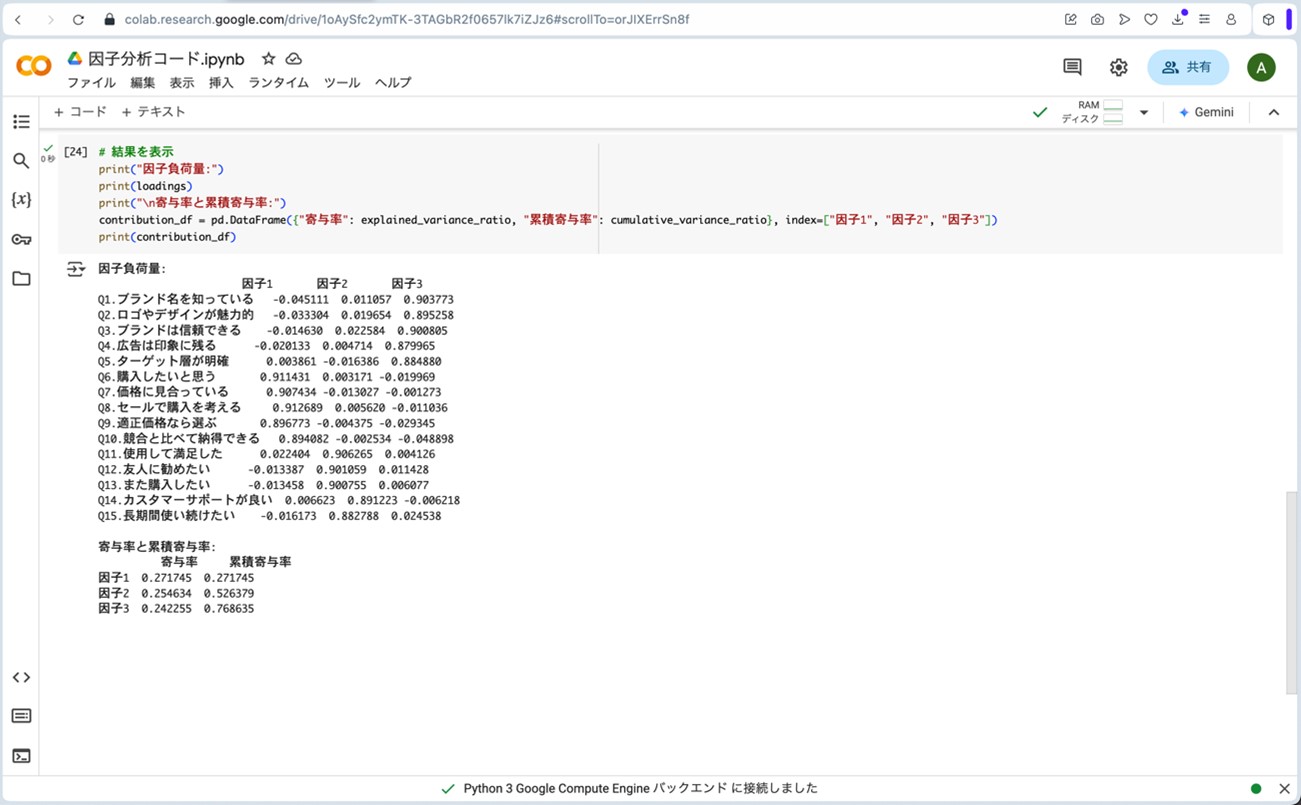
図13.拡大した因子分析の結果

上記因子分析の結果をコピー&ペーストしてExcel等で整形すると、先述の表2にもある以下の結果と一致します。

Googleドライブを利用される際はこちらをご確認、ご理解の上ご利用ください。

Google ドライブ利用規約

ドライブにおけるユーザーのプライバシー保護とユーザー自身による管理
Google ドライブ ヘルプ

※Googleドライブの説明に使用している各図は、Googleのウェブページを撮影して掲載しています。

1. 所属等は執筆当時のもので、現在とは異なる場合があります。
2. また記事中の技術、手法等については、今後の技術の進展、外部環境の変化等によっては、実情と合致しない場合があります。
3. 各記事における最新の動向につきましては、当社までぜひお問い合わせください。

著者プロフィール

プロフェッショナルズストラテジックプランニング局データソリューション部渡邉 成（わたなべ あきら）

この人の書いた記事

• 連載！データ分析③：ロジスティック回帰分析
• 連載！データ分析②：回帰分析
• 連載！データ分析①：相関係数

得意領域

• #データアナリシス
• #機械学習
• #デジタル

著者について詳しく見る